PROBLEM LINK:
Author:Constantine Sokol
Tester:Mahbubul Hasan
Editorialist:Jingbo Shang
DIFFICULTY:
Easy
PREREQUISITES:
Combination
PROBLEM:
For each of 2^K players labeled by 1 .. 2^K, how many permutations of their initial positions can allow him to advance to the final? The tournament is as following figure. The winner of a match is the one with larger label.
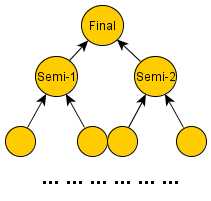
EXPLANATION:
For a given player X, if he advanced to the final, his label should be the greatest among the players in his semi-final part.
Assume he is the winner of semi-final one. His position has 2^(K-1) choices. And, there are X-1 players with smaller label. Therefore, the answer is 2^(K-1) * (X-1) * (X-2) * .. (X - 2^(K-1) + 1) * (2^(K-1))!.
With X varying from 1 to 2^K, it is easy to maintain the product (multiply a number and divide a number), because the MOD number is a prime, according to the Euler Theorem.
If we calculate the inverse by the fast power, similar to the fast multiply I mentioned in a previous editorial, we can get a O(2^K * K) algorithm.
AUTHOR'S AND TESTER'S SOLUTIONS:
Author's solution can be found here.
Tester's solution can be found here.