Problem Link

Practice

Contest

Author:Rahim Mammadli

Tester:Misha Chorniy

Editorialist:Bhuvnesh Jain

Difficulty

EASY-MEDIUM

Prerequisites

Cross Product, Binary Search

Problem

Given a stationary point $P$ and a point $Q$ moving in straight line, indicate the time when $Q$ is visible from $P$, given that there am opaque sphere between them.

Explanation

We will try to find the solution in 2-D and then extend the idea to 3-D as well.

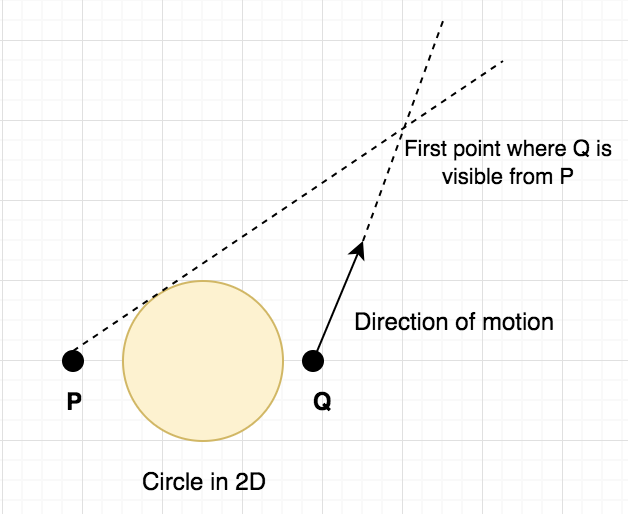
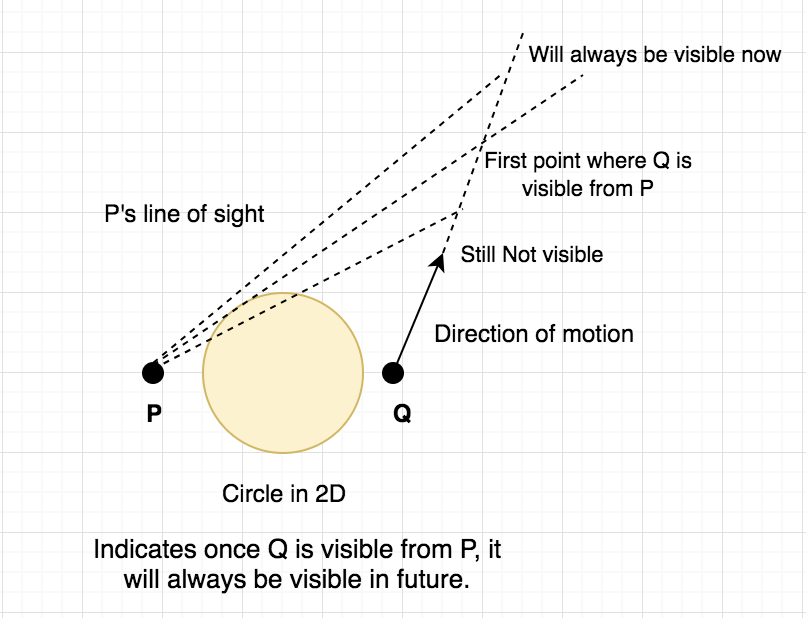
From the above figure, the first idea which can be clearly concluded is that, once point $Q$ becomes visible from $P$, it will remain visible forever. Before that, it will always remain invisible. This, the function (whether $Q$ is visible $P$ at given time $t$) follows the idea that it is false initially and after a certain point, it always remains true. This hints that we can binary search on the answer and just need to check whether the point $Q$ is visible from $P$ at given time $t$ or not. For more ideas on "Binary search" on such type of problem, refer to this awesome tutorial on topcoder. Hence, solution template looks like:

    double low = 0, high = 10^18
    for i in [1, 100]:
        double mid = (low + high) / 2
        if visible(P, Q, C, r, mid):
            high = mid
        else:
            low = mid
    double ans = (low + high) / 2

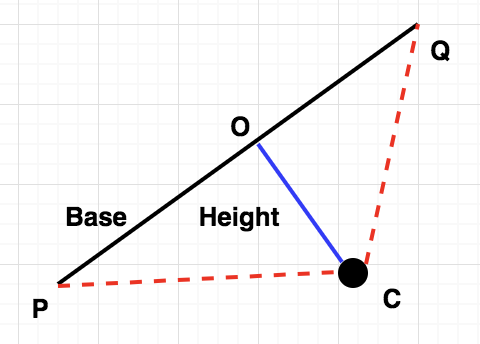
So, given a particular time $t$, we can first calculate the position of point $Q$. Join $P$ and $Q$ by a straight line. If the line doesn't pass through the circle, the point $Q$ is visible from $P$ else it is not visible. To check if a given line passes through the circle or not, it is enough to check that the perpendicular distance of the line from the centre, $C$, of the circle is greater than the radius, $r$, of the circle. For this, we first complete the triangle $PCQ$ and let the perpendicular distance of $PQ$ from $C$ be denoted by $CO$. Using the formula,

$$\text{Area of triangle} = \frac{1}{2} * \text{Base} * \text{Height} = \frac{1}{2} * CO * PQ$$

Since the area of the triangle can be found given 3 points in 2-D, and $PQ$ is the Euclidean distance between $P$ and $Q$, we can find the value of $CO$ efficiently. Finally, we just need to compare it to $r$, the radius of the circle.

For extending the solution in 3-D, the idea is same and we just need to find the area of a triangle in 3-D. For details, one can refer here. It can be clearly seen that the above formula holds for the 2-D case as well.

$$\text{Area of triangle in 2/3-D} = \frac{|CP X CQ|}{2}$$

where $CP$ and $CQ$ are vectors, $a X b$ denotes cross product of vectors and $|a|$ denotes the magnitude of vector.

Thus, to find the length of $CO$, we have

$$|CO| = \frac{2 * \text{Area of triangle PCQ}}{|PQ|} = \frac{|CP X CQ|}{|PQ|}$$

For more details, you may refer to the editorialist solution which exactly follows the above idea.

Extra Ideas/Caveats

The binary search implementation mentioned in the editorial is different from the one mentioned in Topcoder tutorial. Though both will give AC here, the one in Topcoder needs one to correctly set the Epsilon value for termination condition and sometimes can lead to wrong answers due to precision issues. The editorialist just prefers the above style to implement binary and ternary search involving doubles as calculation of epsilon is not required.

Note from the author

Finding the distance of a point from a line in 3-D is a generally common problem and also contains some edge cases where the point may not lie within the line segment region. But given the constraints of the problems, there are no edge cases but we should be aware of it in general.

Feel free to share your approach, if it was somewhat different.

Time Complexity

$O(1)$ per test case (around 100 iterations for binary search).

Space Complexity

$O(1)$

AUTHOR'S AND TESTER'S SOLUTIONS:

Author's solution can be found here.

Tester's solution can be found here.

Editorialist's solution can be found here.