Hey Codechef can u please tell me the way to solve this question http://codeforces.com/contest/893/problem/C without using the BFS DFS search and SIMILARITY PROPERTY as provided in their contest tutorials ... I just want to solve it using iterative way can anyone plzz tell me the way how to store all the nodes (characters in the above ques) in just one location (by using vector of vectors) and then iterate over it for each corresponding vector[i] representing the path starting from the i th node ANY HELP WILL BE APPRECIATED !!!

I wish to know, as I'm sure many other users, about the further schedule of scholarships for CCDSAP for Jan 21 exam date.

My questions are:

1. Will there be a scholarship for Jan 21 exam date?
2. If Yes, what will be the selection criteria? December long challenge or January Long challenge or Both?
3. And, will the previously selected candidate will be eligible to be selected again?

Waiting for your reply. :)

@admin@vijju123

can any one explain y im getting WA ?

code : https://www.codechef.com/viewsolution/16384002

Hello Codechef Community,

I had earlier recorded my thoughts about the online round, and the subsequent calls for a "recontest" , here (LINK)

With some of the regional sites releasing the results today, I just thought I'd record my conception of the same here.

Amritapuri has 250 slots, and almost 230-240 unique colleges have been invited. This is ABSURD! Yes, the spirit of ICPC is to spread the idea of programming far and wide, but is this move going to backfire in the long run? There are teams who have secured a rank > 2000 in the list and qualified, but teams that came within 100 ranks in the original rank list, lose out simply because they couldn't attain the "college first" rank.

I, for one, gave Competitive Programming my everything for the past one year, in the hope of performing well in ICPC. There are many many others who do the same, but ultimately lose out on this because of this dubious selection criteria.

What happens if they give up on competitive programming because of this? I know there's an argument that one shouldn't materialistically do CP for the purpose of results in contests, but come on! Losing a coveted spot at the regionals because of no fault of theirs, seems to be extremely hard to digest.

Maybe having a certain slot (50-60% of the seats) reserved for the college-first teams, and giving the rest to other well performing colleges ought to be an option. But not many regionals seem to be following this, this is a huge loss to the community.

With the selection of online round questions being a little queer, and selection criteria becoming a tight leash, ICPC is losing its sheen in my opinion.

Hello,

I continue to report every mistake that I find along the way... :) This time there is a minor error in the sample input of the problem https://www.codechef.com/problems/G1 The number of the test cases should be 3, not 2.

I am new to this karma system, Can you explain me why is it called so? What has karma points got to do with contribution?

HEAPULM problem from Spoj can be solved by recursion, by making binary search tree of nodes of sorted priority and then performing an inorder traversal of the BST. But how can it be solved by using segment tree? This problem is categorized under segment tree inpraveendhinwa's blog

Problem Link

Practice
Contest

Difficulty:

CAKEWALK

Pre-requirements:

Simple Arithmetic

Problem:

Chef has N cupcakes, which he wishes to package. He makes as many packages of a fixed size as possible from the N cupcakes. After he has made these packages, he eats the remaining. Find what size of package (A) will ensure that he gets to eat the maximum possible number of cupcakes. If there is a tie, determine the largest such package-size.

Quick Explanation:

Given the size of the package A, the number of cupcakes Chef will get to eat will be N % A. Let us denote the optimal size by A#. A# is then [N/2]+1, where [x] is floor(x).

To see the proof of this, firstly note that [N/A#] = 1. If not, let k = [N/A#] > 1. Assuming that Chef uses size A#, he gets N - k * A#. If Chef had used A = k * A#, then too he would have got N - k * A#. And in deciding between these two which to choose, he would choose the larger, this means that he would have rather chosen "k * A#" instead of A#, thus contradicting that [N/A#] > 1.

Now, [N/A#] = 1 <=> A# > N/2, and that the amount Chef gets to eat = N - A#.

This is maximum for A# = "least integer > N/2" = [N/2] + 1.

Detailed Explanation:

In order to solve this question, we first need to ask ourselves, "if I were the Chef, and I were to use a package-size of A, how many cupcakes would I get to eat?"

If we can answer this question, it will give us an idea of what could possibly be the optimal A. In fact, the answer to the above question, is merely N % A. This is because Chef keeps on taking out cupcakes in groups of A to package, so the number of cupcakes he has left follows the sequence N, N-A, N-2A, …, N - k * A, where after taking out k packages, we have N - k * A < A. This is precisely N % A.

Approach 1:

This approach is exactly as described under "Quick Explanation".

Claim: Chef will make only a single package in the optimal size (after getting rid of ties).

To illustrate the proof as given earlier, let us assume N = 15. Now,

• A = 2, chef uses up 14 cupcakes in his package. He might as well have chosen his package size as A=14 here.
• A = 3, chef uses up 15 cupcakes in his package. He might as well have chosen his package size as A=15 here.
• A = 4, chef uses up 12 cupcakes in his package. He might as well have chosen his package size as A=12 here.

In this manner, so long as his chosen package size allows for more than 1 package, then he might as well have chosen his package size correspondingly larger : [N/A]*A to be precise.

The above puts a lower-bound on the optimal package size (A#), namely > N/2. Also, given this size A#, the remaining cupcakes is exactly N-A#. Maximizing this quantity subject to A# > N/2 gives us A# = "least integer > N/2" = [N/2] + 1.

Approach 2:

In this approach, let us first investigate what happens to the number of remaining cupcakes (lets denote it by f(A)) as a function of A. If we were to try simple values of A to see what happens, we get

1. for A = 1, Chef has 0 cupcakes left.
2. for A = N, Chef has 0 cupcakes left.
3. for A = 2, Chef has 0 or 1 cupcakes left (depending on whether N is even or odd).
4. for A = N-1, Chef has 1 cupcake left. and so on.

The above discussion qualitatively gives us the following ideas: If A is too small, then f(A) is also small (bounded by A). If A is too large, then f(A) is again small since we've already used up cupcakes in the package itself.

Formally,

1. f(A) < A (N % A < A always)
2. f(A) <= N - A (since A <= N, we take out at least one package).

Armed with the above two observations, we get that f(A) < N/2 irrespective of whatever size we choose: this is seen by summing the 2 inequalities above, giving us 2 * f(A) < N => f(A) < N/2.

Further, the bounds given above suggest that they will be weakest when A ~ N/2: the bounds can be written as f(A) <= min(A-1, N-A), where the term on the RHS is largest when A = (N+1)/2. The above shows us a Necessary condition on the number of remaining cupcakes: f(A) < N/2.

Finally, if A <= N/2, then the bound "remaining <= N-A" wouldn't be strong, since we could take out 2 packages, giving us remaining <= N-2A; however if A > N/2, then we get that f(A) = N - A. Thus, choosing A = [N/2] + 1, which is the least integer > N/2, we would get f(A) = (N-1)/2 (for odd N), = N/2 - 1 (for even N) which are in both cases the largest integer < N/2. This shows us a Sufficient condition on the number of remaining cupcakes: that it is Possible to get "the largest integer < N/2" as our answer.

In other words, we have found a necessary and sufficient condition proving that A = [N/2] + 1 is the optimal package size.

Author's Solution:

Can be found here

Tester's Solution:

Can be found here

I need help in debugging macro. Macroprocessor expands all the macros before compilation.
So after macro expansion, d1 and d2 should behave exactly same, but they don't. Why?!
d1(1); will be expanded as it is. For d2(2); only d2(2) will be expanded and will have a semicolon at the end(which was not part of macro).
What is going wrong here? Please help.

Code -

include<iostream>
define d1(i); cout<<i;
define d2(i) cout<<i
using namespace std;
int main(void){
    if(true==false) d1(1);
    if(true==false) d2(2);
    return 0;
} 

Expected output -

Output -
1

Expected code after preprocessing -

{<iostream> code}
using namespace std;
int main(void){
    if(true==false) cout<<1;
    if(true==false) cout<<2;
    return 0;
}

Its been almost 10 days since ZCO 18, there was some unofficial info that the results will be published after 10 days. Hence when are the results expected to be out ?

Problem Link

Practice
Contest

Setter:Hasan Jaddouh
Tester:Amr Mahmoud
Editorialist:Bhuvnesh Jain

Difficulty

EASY-MEDIUM

Prerequisites

Strongly Connected Components, Bfs / Dfs

Problem

Find the minimum number of cells to select in a matrix so that we can reach every cell from it through a series of moves which is, "You can move from one cell to another only if they are adjacent (i.e. share a side) and the height of destination cell is not more than height of current cell."

Explanation

The edges in the graph will be between cells $(i, j)$ and $(x, y)$, only if they share a side. Also, the edges will be directed as the edge exists from a cell into another only if the height of destination cell is not less than the height of the current cell.

For example in the sample input 1, the edges will be as follows:

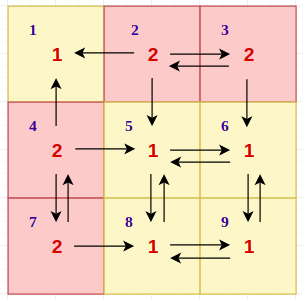
Now given a directed graph, we want to select a set of cells so that all cells are reachable from it. The first observation is 2 decompose the graph into Strongly connected components, as there may be cycles in the graph. This is because all the vertices in a cycle can be visited by starting from any vertex.

Now, we have a directed graph in which there are no cycles. (It is also called a DAG). In this graph, we claim that we chose only vertices with indegree $0$ to be in our set as the possible candidate solution.

Reason : Let us say there is an edge $P$ to $Q$ in the DAG. Let us denote the set of vertices reachable from $Q$ to be $S$. Then all vertices in $S$ are also reachable from $P$. But $P$ is not reachable from $Q$. So continuing this process, we will see that only vertices having indegree $0$ are not reachable from any other vertex but they as a set cover all the vertices reachable from it.

The DAG of input sample 1 is give below:

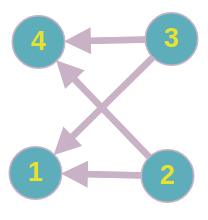
In the above figure, $1$ represents the set ${1}$, $2$ represents the set ${2,3}$, $3$ represents the set ${4,7}$ and $4$ represents the set ${5,6,8,9}$.

Thus, the algorithm is as below:

1. Construct the directed graph from the grid. Complexity is $O(N * M)$. Also, the number of edges in the graph is bounded by $(8 * N * M)$ as each cell can have at most 4 neighbors and it can have edge in both directions.
2. Decompose the graph into one with no cycles. You can use Tarjan's algorithm or Kosaraju algorithm for this step.
3. Find the number of vertices with indegree $0$ in DAG.

Author's Solution

The solution counts the number of components having same heights, such that all adjacent components are less (strictly) than it.

Proof: Each such component consisting of all cells of same height can be represented by 1 cell only. Now, each component can either have all adjacent components less tha it or not. If all cells adjacent to it are smaller, the those can be reached from the current cell, so they are ot counted towards the answer. If we repeat this process, for each component, we are bound to find only those cells which will contribute to the answer. Also, if we assume some cell that shouldn't be in answer was counted by above process, the it would contradict the fact that all adjacent components are lesser than it.

The above process can be simply implemented by a dfs call from every vertex and check if all components adjacent to it are smaller than it or not. For details, refer to author's solution.

Time Complexity

$O(N * M)$, per test case.

Space Complexity

$O(N * M)$

Solution Links

Setter's solution
Tester's solution
Editorialist's solution

Problem Link

Practice
Contest

Setter:Hasan Jaddouh
Tester:Amr Mahmoud
Editorialist:Bhuvnesh Jain

Difficulty

EASY

Prerequisites

Looping Techniques

Problem

Find a suitable match for every person depending on some constraints mentioned in the statement.

Explanation

The solution is simply doing what the problem statement says. Just maintain a "wait" variable for all players, which when set to $1$ means that the player is still waiting for his chance to pair up with someone, and $0$ meaning that the person is already paired up.

Thus, for every player, we start from the first person and proceed in increasing order of their times of arrival and break as soon as we get some matching person whose "wait" variable was set to "1".

To check if any person matches with someone else, we can simply use "if" statements to check the conditions mentioned in the statement.

1. The first condition can be checked as follows : $y <= x \\text{ and } x <= z$, meaning that $x$ lies in the range $[y, z]$
2. The second and third condition can be simply checked by comparing the 2 values i.e. time and "rated/unrated" criteria.
3. For last condition, we first check to which category it belongs i.e. $\\{ \\text{random, black, white} \\}$. Then as per the category, we do the corresponding check for the other player i.e. "random" matches with "random", "black" with "white" and "white" with "black".

Time Complexity

$O(N^2)$, per test case.

Space Complexity

$O(N)$

Solution Links

Setter's solution
Editorialist's solution

I am getting runtime error. help?

link https://www.codechef.com/viewsolution/16386878

i am getting sigsev error in lr query using segment tree please help.https://www.codechef.com/viewsolution/16387107

Sadly, I am facing a dilemma.

I made a big mistake and the payment for my team is still not done. I was busy with my majors and I tried doing the payment today and the SBI account didn't update the beneficiary and long story short I still have not done the payment.

What I didn't consider was tomorrow was the last Saturday and NEFT will go through only on Monday.

What should I do now? I have mailed AmritaPuri and is there any chance that I will get a extension till Monday?

(I know this is a big *** up but any help will be highly appreciated)?

Edit:-

Thanks for helping out guys. I mailed AmritaPuri and they told me to go forward with IMPS. I did that and my payment was later confirmed on Monday(27-11-2017). :)

Personally I think the question were a little harder than previous years. I managed to finish in 2hrs.
First problem was prefix sums+ maths
Second was greedy + implementation

Please share your answers for ZIO here... And tell what cutoff you expect I personally found it easy..(similar to last year) and expect the cutoff to be around 50-55 Until now, these are the answers I can almost confirm,

1. 74
2. 67
3. 65
4. 3
5. 2
6. 4
7. 20
8. 16
9. 96
10. 49
11. 261
12. Too many different answers

PS:

ZIO Results announced: https://www.iarcs.org.in/inoi/2018/zio2018/results_zio2018.php

ZCO Results announced: https://www.iarcs.org.in/inoi/2018/zco2018/results_zco2018.php

Official Solutions(ZIO) and cutoff: https://www.iarcs.org.in/inoi/2018/zio2018/zio2018-solutions.pdf

Hope you got selected:)

PROBLEM LINK:

Practice
Contest

Author:Misha Chorniy
Tester:Sergey Kulik
Editorialist:Pawel Kacprzak

DIFFICULTY:

CAKEWALK

PREREQUISITES:

basic math

PROBLEM:

Given integers a, b, c, d find the number of integer solutions of inequality x < y, where a ≤ x ≤ b and c ≤ y ≤ d. In one test file there are several test cases to handle.

QUICK EXPLANATION:

Iterate through all possible values of x and for each one, count the number of valid values of y to pair with it.

EXPLANATION:

Subtask 1

In the first subtask, we know that a, b, c, d ≤ 10³. For such low constraints, it can observed that in any valid pair of x < y, both x and y are less or equal than 10³ as well. With this observation, it is possible to iterate over all possible x, y ≤ 10³. Thus, for each fixed pair x, y, we can explicitly check if x < y and add 1 to the result if the inequality is fulfilled.

Subtask 2

In the second subtask we have a, b, c, d ≤ 10⁶, so iterating over all possible values of x and y explicitly is not possible here. However, constraints are small enough to iterate over all possible values of one of the variables. Let’s say that we are going to iterate explicitly over all possible values of x. For one such fixed value of x, the problem reduces to how many values of y are there such that c ≤ y ≤ d and x < y. In other words, the task is to count the number of integers y, such that y ≥ max(c, x + 1) and y ≤ d. Let’s assume that c ≤ d, otherwise, there are no valid values of y of course. It follows, that for a fixed x, there are d - max(c, x+1) + 1 valid values of y, because the number of integers in a range [R₁, R₂] is given by R2 - R1 + 1.

The final result is the accumulated result for each possible value of x computed as described above. Total time complexity of this method is linear in terms of the number of possible values of x, which is at most 10⁶.

AUTHOR'S AND TESTER'S SOLUTIONS:

Setter's solution will be uploaded soon.
Tester's solution can be found here.
Editorialist's solution can be found here.

Raja loves Strings. In Strings he specially loves palindromes.Palindromes are strings that read the same when read forward or backwards. Here Palindromes considered are only of even length(maybe 0). His Teacher gave me him a long string consisting of only digits as a gift on his birthday. Now Raja wants to know The longest subarray whose elements (i.e digits) can be rearranged to form a palindrome of even length. Raja is unable to figure out the solution to the problem so he asks for your help.

INPUT SPECIFICATION - The function contains one argument - A String S consisting of digits (0-9). First and only line of input consists of S (1 <= |S| <= 100000). OUTPUT SPECIFICATION - You must return a single integer denoting the longest subarray whose elements (digits) can be rearranged to form a palindrome of even length.If no such subarray can be found return 0. Example - Sample Test Case 1

Input

12345354987

Output

6 Explanation : No subarray can be rearranged to form even length of palindrome .Hence 0.

Explanation : Here the longest subarray is 345354 which can be rearranged to form 345543 which is a palindrome of even length 6.Hence and is 6.

Sample Test Case 2-

Input

12345

Output

0

. You are given a file which contains a very bit sequence of 0 and 1 and it is sorted. Hence all the zeros are in front of the ones.One needs to find the first orrcurance of of 1 in the file(return the position).

The only method to access the file is through a method whose signature is — int getBitAtPosition(int position) — which returns the bit at the specified position in the file.

I thought of using a binary search till the 1 is not found ....once it was found we can keep on decreasing the position linearly and saving the previous value so that if the bit at pos-- is 0 then we can get the position as pos