I know how to solve this problem Perfect Number in a brute force way but the tags on that page show binary search and DP as well. I am curious to know how this problem can be solved using Binary search and DP. Can someone help me with this please?
Help needed with codeforces problem?
Can anyone help me with Disciple Training from Coder's Legacy 2016 Contest?
Hello friends can someone tell me how to approach this problem ??
@vijju123@kaushal101@mohit_negi@taran_1407@vivek_1998299@meooow@john_smith_3
How to delete one of my teams and get my handle renamed to the team's handle?
I have been trying to find a way to delete a team which I created long back and rename my handle to the handle of the team. I am unable to find a way to do so. My handle is "shubhambajpai" and my team's handle is "ahamshubham". Is there a way to do so? Please help.
BROCLK - Editorial
PROBLEM LINK:
Author:Trung Nguyen
Tester:Hanlin Ren
Editorialist:Hanlin Ren
DIFFICULTY:
MEDIUM
PREREQUISITES:
Trigonometry, Fast Matrix Exponentiation, Modular Inverse
PROBLEM:
A clock has a minute hand which goes $x$ angle per second. The minute hand has length $l$ and the center of clock has coordinate $(0,0)$. Initially, the other endpoint is at coordinate $(0,l)$, and after $1$ second its $y$-coordinate becomes $d$. Given $l,d,t$($x$ is unknown), calculate the $y$-coordinate of this endpoint after $t$ seconds.
QUICK EXPLANATION:
By the problem statement we have $\cos(x)=d/l$, and the final answer is $\cos(tx)\cdot l$. So we only need to compute $\cos(tx)$. There is a formula computing $\cos(nx)$: $$\cos(nx)=2\cos(x)\cos((n-1)x)-\cos((n-2)x),$$ and we can use fast matrix exponentiation to compute $\cos(tx)$ in $O(\log t)$ time.
EXPLANATION:
A note to modular arithmetic
Setter's Solution
First notice that $x$ is given by $\cos(x)=d/l$. To see this, consider the following figure which illustrates the problem statement: $OA$ and $OB$ are the position of minute hand initially and after $1$ seconds, respectively.
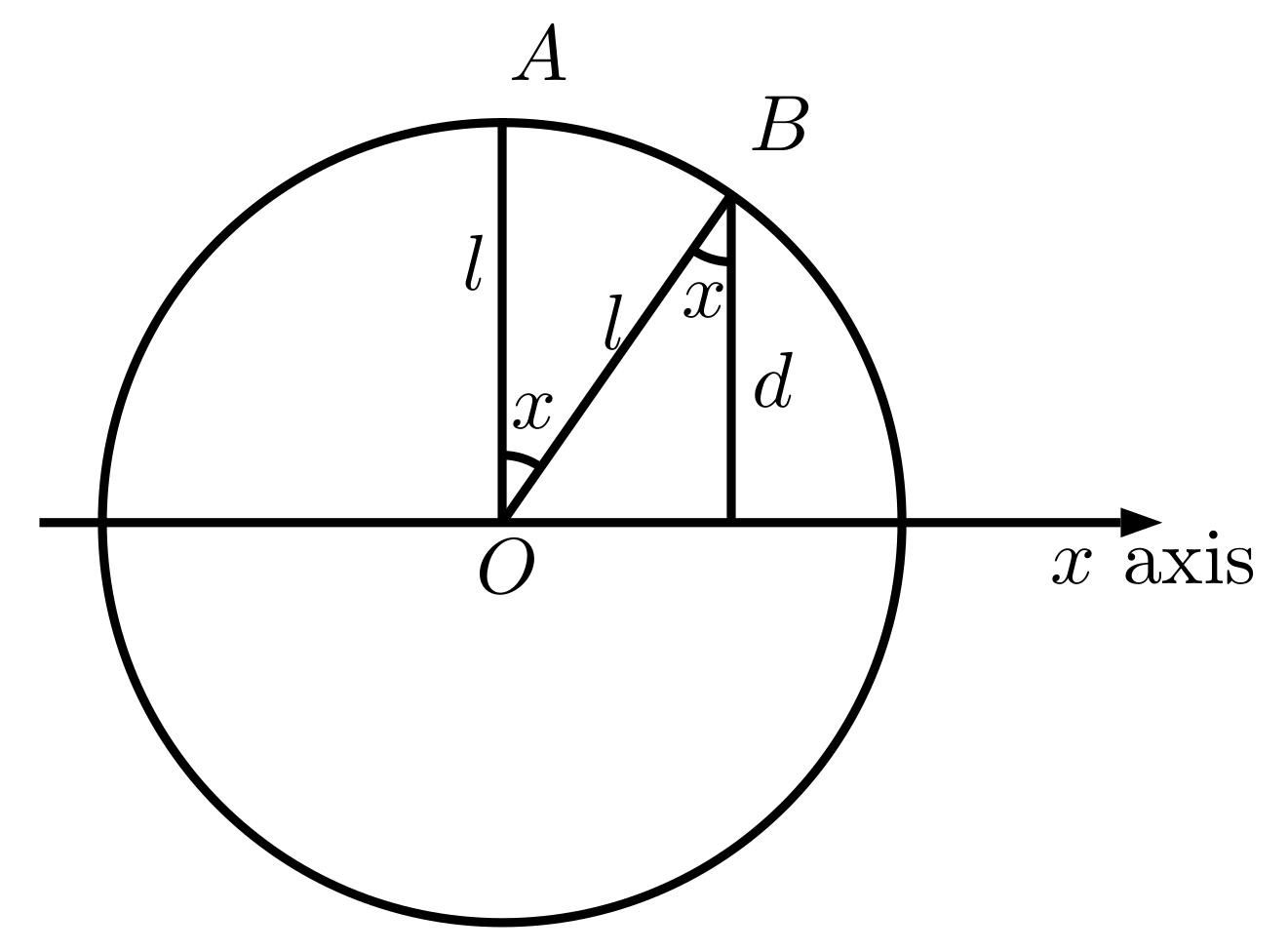
And the answer after $t$ seconds is $\cos(tx)\cdot l$. Therefore, our actual task is: given $\cos(x)$ and integer $t$, compute $\cos(tx)$.
Notice the following formula: $$\cos(nx)=2\cos(x)\cos((n-1)x)-\cos((n-2)x)\ \ \ (*)$$ that means we can write $\cos(tx)$ in a matrix-multiplication form: $$\begin{pmatrix}\cos(tx)\\\cos((t-1)x)\end{pmatrix}=\begin{pmatrix}2\cos(x)&-1\\1&0\end{pmatrix}\begin{pmatrix}\cos((t-1)x)\\\cos((t-2)x)\end{pmatrix},$$ and therefore $$\begin{pmatrix}\cos(tx)\\\cos((t-1)x)\end{pmatrix}=\begin{pmatrix}2\cos(x)&-1\\1&0\end{pmatrix}^{t-1}\begin{pmatrix}\cos(x)\\1\end{pmatrix}.$$ Thus we can compute $\cos(tx)$ by fast matrix exponentiation in $O(\log t)$ time.
Tester's Solution
Again, we're given $\cos(x)$ and integer $t$ and we want to compute $\cos(tx)$. But what if we don't know formula $(*)$? We can use the following (better-known) formula: $$\begin{align*} \cos(a+b)=&\cos(a)\cos(b)-\sin(a)\sin(b)\ \ \ (1)\\ \sin(a+b)=&\sin(a)\cos(b)+\cos(a)\sin(b)\ \ \ (2) \end{align*}$$
All numbers we come across will be in the form $a+b\sin(x)$. Although we don't know $\sin(x)$, we can represent such a number as $(a,b)$. Therefore we can define $+,-,\times$ on these numbers: $$\begin{align*} (a,b)\pm(c,d)=&(a\pm c,b\pm d)\\ (a,b)\cdot(c,d)=&(a+b\sin(x))(c+d\sin(x))\\ =&ac+bd(1-\cos^2(x))+(ad+bc)\sin(x)\\ =&(ac+bd(1-\cos^2(x)),ad+bc). \end{align*}$$
We can write a recursive procedure $\mathrm{Solve}(t)$ for computing the pair $(\cos(tx),\sin(tx))$.
- If $t=1$, we return $\cos(tx)=(\cos(x),0)$ and $\sin(tx)=(0,1)$;
- If $t$ is odd, then we find $(\cos((t-1)x),\sin((t-1)x))$ by calling $\mathrm{Solve}(t-1)$, and $(\cos(tx),\sin(tx))$ can be computed by formula $(1)$ and $(2)$;
- If $t$ is even, then we call $\mathrm{Solve}(\frac{t}{2})$ to find $(\cos(\frac{t}{2}x),\sin(\frac{t}{2}x))$, and $(\cos(tx),\sin(tx))$ can be computed similarly.
This procedure runs in $O(\log t)$ time since every two steps decrease $t$ by half.
Suppose we've computed $\cos(tx)=(a,b)$. $b$ must be equal to $0$ since it's possible to represent $\cos(tx)$ by only $\cos(x)$ terms. Therefore $\cos(tx)=a$ and we're done.
On formula $(*)$
How to prove formula $(*)$? In fact I don't know, but one might look into this page for answer. The Chebyshev polynomial of the first kind is defined as $T_0(x)=1$, $T_1(x)=x$ and $T_{n+1}(x)=2xT_n(x)-T_{n-1}(x)$. It can be proved that $T_n(\cos(x))=\cos(nx)$, which directly implies formula $(*)$.
ALTERNATIVE SOLUTION:
Please feel free to share your approach :)
AUTHOR'S AND TESTER'S SOLUTIONS:
Author's solution can be found here.
Tester's solution can be found here.
RELATED PROBLEMS:
Help : Unknown Compilation Error
Can you please help me to find and debug error https://www.codechef.com/view/ICL2018/error/17560172 in https://www.codechef.com/viewsolution/17560172
Although I then used DMA to get rid but really wanted to know what was the actual error in this. And that too compilation error.I can't cross the Highway...Help!
With regard to this time's Long Challenge and the question Highway crossing.
I feel that I have got my logic on point but seem to be missing some minute detail. I pass all the tests except the second subtask's second part. I feel my code is almost self explanatory.
I've gone over my code about 20 times but can't see what I'm missing!
I've solved taking normal X,Y axis with cars moving on X axis and Chef going downwards in negative Y direction hence the coordinates.
The submission link as well - https://www.codechef.com/viewsolution/18214679
Thanks In Advance :)
#include <iostream>
#include<stdio.h>
#include<bits/stdc++.h>
#define ll long long int
#define li long int
using namespace std;
int main()
{
ios::sync_with_stdio(0);
ll t;
cin>>t;
while(t--)
{
//double g=-10000000000.12432;
//cout<<setprecision(16)<<g;
ll n,s,y;
cin>>n>>s>>y;
double time_to_cross_lane=double(y)/double(s);
vector<ll> velocities(n);
vector<ll>directions(n);
vector<ll>positions(n);
vector<ll>lengths(n);
for(ll i=0;i<n;i++)
{
cin>>velocities[i] ;
}
for(ll i=0;i<n;i++)
{
cin>>directions[i] ;
}
for(ll i=0;i<n;i++)
{
cin>>positions[i] ;
}
for(ll i=0;i<n;i++)
{
cin>>lengths[i] ;
}
double total_time=0.0;
for(ll i=0;i<n;i++)
{
//left to right
if(directions[i]==1)
{
// coordinates of car. left and right at any time
double left_coordinate =(positions[i]-lengths[i])+velocities[i]*(total_time);
double right_coordinate =(positions[i] )+velocities[i]*(total_time);
// case 1 not hitting
if(left_coordinate>=0 && right_coordinate>=0)
{
total_time+=time_to_cross_lane;
continue;
}
//case 2
else if(left_coordinate<=0 && right_coordinate>=0)
{
total_time+=(double(-left_coordinate)/double(velocities[i])) + time_to_cross_lane;
continue;
}
//case 3
else if(left_coordinate<=0 && right_coordinate<=0)
{
double time_to_reach_for_car=(double(-right_coordinate)/double(velocities[i]));
double time_to_cross_length = double(lengths[i])/double(velocities[i]);
// if car reaches before chef would cross the lane
if( time_to_reach_for_car<=time_to_cross_lane)
{
total_time+=time_to_reach_for_car+time_to_cross_length+time_to_cross_lane;
}
else
total_time+=time_to_cross_lane;
}
// if a coordinate is zero
else if( left_coordinate==0 || right_coordinate ==0 )
{
if(left_coordinate==0)
{
total_time+=time_to_cross_lane;
}
else if(right_coordinate==0)
{
total_time+=time_to_cross_lane+(double(lengths[i])/double(velocities[i]));
}
}
else
total_time+=time_to_cross_lane;
}
//right to left
else if(directions[i]==0)
{
double left_coordinate =(positions[i])-(velocities[i]*total_time);
double right_coordinate =(positions[i]+lengths[i])-(velocities[i]*total_time);
// case 1 not hitting
if(left_coordinate<=0 && right_coordinate<=0)
{
total_time+=(time_to_cross_lane);
}
else if(left_coordinate<=0 && right_coordinate>=0)
{
total_time+=(double(right_coordinate)/double(velocities[i]) + time_to_cross_lane);
}
else if(left_coordinate>=0 && right_coordinate>=0)
{
double time_to_reach_for_car=(double(left_coordinate)/double(velocities[i]));
double time_to_pass =(time_to_reach_for_car+( double(lengths[i])/double(velocities[i])));
//car would reach before chef would cross lane
if( time_to_reach_for_car<=time_to_cross_lane)
{
total_time+=(time_to_pass+time_to_cross_lane);
}
else
total_time+=(time_to_cross_lane);
}
//coordinate is zero
else if(left_coordinate==0||right_coordinate==0)
{
if(left_coordinate==0)
{
total_time+=(time_to_cross_lane+( double(lengths[i])/double(velocities[i])));
}
else if(right_coordinate==0)
{
total_time+=(time_to_cross_lane);
}
}
}
}
cout<<fixed<<setprecision(12)<<total_time<<'\n';
}
return 0;
}
Bug in April18 ratings update
@admin Again posting it. https://discuss.codechef.com/questions/124629/fixedbug-in-cook92b-ratings-
Same issue still persist. Original question is closed so I cannot comment there. Today I saw something unusual. First page was updated because My rating Increased to 5 star so I took its screenshot. But Then issue is back. Please check time in 2 screenshots. Also my 4 star page shows highest rating 2016. But I have not suffered a rating loss after April18A.


[When ??]SnackDown' 18
@admin , Is snackdown scheduled this year ?? As I can see https://www.codechef.com/snackdown/2017/schedule Registration for snackdown'17 started on 14 April'17. But for this year It's 18 today and I am not seeing any promotions/ads/anything else for snackdown'18. I'm eagerly waiting for it. Because it will be my first snackdown. If it's not scheduled this year then please schedule it.
Minor Bug. Seen While commenting.
@admin One more minor bug/error. I recently made a comment. And as soon it is posted. My 4 star are not visible beside it. And this is only visible when I refresh the page.

CLERVT - Editorial
PROBLEM LINK:
Author and Editorialist:Soumik Sarkar
Tester:Sarthak Manna
DIFFICULTY:
MEDIUM
PREREQUISITES:
Euler tour, Dynamic programming
PROBLEM:
There is a tree with $N$ vertices, and a set of vertices $G$. For every subset $G'$ of $G$, find the maximum number of edges which can be removed while leaving each vertex in $G'$ connected to vertex $1$. Calculate the XOR-sum of all these values.
EXPLANATION:
Consider the tree to be rooted at $1$. Given a set $G$ imagine you have removed all edges are not necessary for the vertices in $G$ to remain connected to $1$. What will this graph look like?
Of course the graph will remain a connected tree. Also, all the leaves will belong to $G$. Some elements of $G$ may lie in the interior of the tree as well. If asked to find the number of edges in this tree, you would say the answer is $|G| - 1$. However, in a roundabout way I can also claim that counting the edges on an Euler tour of this tree will give me exactly twice the answer.
Let it be that during the Euler tour I start from the root and happen to visit the vertices in $G$ in the order $G_1, G_2, G_3, ... G_K$. I can say the total length of the Euler tour is $dist(1, G_1) + dist(G_1, G_2) + dist(G_2, G_3) + .... + dist(G_K, 1)$. As mentioned before, this is exactly twice the number of edges in the tree, but the values of all these terms are the same as in the original tree. So if we know $dist(G_i, G_j)$ for each pair $(i, j)$ and also the "Euler tour order" of the vertices in $G$, we can calculate the answer in $\mathcal{O}(K)$!
We can get the Euler tour order with one dfs from the root. And then we can proceed to make $K$ dfs from each vertex in $G$ to calculate the distance matrix for each pair of vertices in $G$. To get the distance matrix it is also possible to use faster methods, but not necessary.
However applying this procedure in this form is too slow as it requires $\mathcal{O}(K)$ time ($K/2$ on average) for each subset of $G$.
To optimize it, we can notice that we can use the answer for one subset to calculate that of another. Let us denote by $f(G)$ the value $dist(1, G_1) + dist(G_1, G_2) + ... dist(G_{x-1}, G_{x})$ where $G_1$ to $G_x$ are the elements of $G$ in Euler tour order. Then clearly $f(G) = f(G \setminus G_x) + dist(G_{x-1}, G_{x})$. Now we can apply dynamic programming using bitmasks to denote subsets and calculate the answer for each subset in constant time and XOR them together.
ans = N - 1
for mask in [1..2^K]:
x = last set bit in mask
if x is the only set bit in mask:
dp[mask] = dist(1, G[x])
ans = ans XOR (N - 1 - dp[mask])
else:
y = second last set bit in mask
dp[mask] = dp[mask \ y] + dist(G[y], G[x])
ans = ans XOR ((N - 1 - (dp[mask] + dist(G[x], 1)) / 2)
Note: The solution requires finding the last (or first) 2 set bits in an integer which can be done quickly in GCC using __builtin_ctz. If you instead find the set bits by looping over each bit position it appears to take $\mathcal{O}(K)$ time for each subset but with a little thought it can be shown that the total operations required over all subsets remains $\mathcal{O}(2^K)$.
Total complexity is $\mathcal{O}(NK + 2^K)$.
ALTERNATE BASIS FOR SOLUTION:
Instead of calculating the answer as half of $dist(1, G_1) + dist(G_1, G_2) + ... + dist(G_K, 1)$ one can also claim that the answer is exactly $dist(lca(1, G_1), G_1) + dist(lca(G_1, G_2), G_2) + ... + dist(lca(G_{K-1}, G_K), G_K)$, where $lca(u, v)$ is the lowest common ancestor of $u$ and $v$. The rest of the process can be done based on this as well.
ALTERNATE SOLUTION:
Instead of storing answers to "What is the tree size for a particular subset?" we can instead store "How many subsets have a particular tree size"? This is a better way because the number of unique sizes is bounded by $N-1$, whereas the number of subsets is much greater.
Let $f(i, d)$ be the number of subsets that have $G_i$ as last element and tree size exactly equal to $d$. Then for any $G_j$ for $j > i$, the value of $f(i, d)$ directly contributes to $f(j, d + dist(lca(G_i, G_j), G_j))$. Here dynamic programming can be used in the "forward" manner, to get a solution in $\mathcal{O}(NK^2)$.
Solution by @uwi: 18276897
Solution by @filyan: 18287756
AUTHOR'S AND TESTER'S SOLUTION:
Author's solution can be found here
Tester's solution can be found here.
Lazy Bartender: Amazon Interview Question | Help
Can someone tell me how to solve this(Lazy Bartender) problem ?
UVA online judge problem
Can someone help me understand this problem on UVA? Don't know why I am getting a Wrong Answer.
Thanks.
CHEFPAR- Editorial
PROBLEM LINK:
Setter-Misha Chorniy
Tester-Misha Chorniy
Editorialist-Abhishek Pandey
DIFFICULTY:
CHALLENGE
PRE-REQUISITES:
Varying. Challenge problem is usually an application of your skills in competitive programming in general.
PROBLEM:
Given an array $A[]$ of randomly generated sequences, we have to add some integer $D_i$ (need not be distinct) to each array element $A_i$, where $0\le D_i\le K$. Our goal is to maximize $\frac{1}{M}\sum_{i=1}^{M} B_i$ where $B_i=(A_1*A_2...*A_N)\%P_i$
QUICK ANALYSIS:
It seemed that contestants faced problems in getting a good solution. We're concluding that, because, Some of the trivial solutions got too high points than what they should have got. Majority of the contestants simply printed back the input, or used $input+rand()\%K$ &etc.
ANALYSIS:
The first thing I want to say is that, this editorial is incomplete. And it will remain so, until you guys dont contribute! Its impossible to have any hard and fast approach for the challenge problems, and for the editorial to be at its full potential, I want to request you guys to discuss your approach. Benefit in challenge problem is better gained by discussion, seeing flaws of your approach and analyzing other's strengths- and seeing what worked well, and to what degree. Hence, I would request the community to put forward their approach and intuition behind the question :).
As for editorial, I will try to discuss some of the approaches I saw, in both div1 and div2. I hope you people like it :)
1. Div2-
Not even 10 minutes passed from start of contest on the historical date of $6th$ $April,2018$ when Div2 had got the first few accepted solutions. I had a guess in mind, and I,curious as a doomed cat, decided to see what they did and confirm my intuition. And I dont know if it was fate, or destiny, or perhaps something else, but what I saw was an exact picture of what I had in my mind...
cin>> arr[i]; //Take array input.
cout<< arr[i];//Print it back.
This approach got something $\approx 85-88$ points. It was $88.7$ when I checked last on $14th$.
Further solutions were also on similar lines. Eg-
cin>>arr[i];
cout<< arr[i]+rand()%k;
This one got $85.8$ points then. Sad luck for that guy :/
cin>>arr[i];
cout<< arr[i]+k;
This solution performed better, and got around$88-89$ points on average.
Some of the better solutions at div2 which got $\ge90$ involved-
- Choose one of the primes. Lets call it $P$ Either largest, smallest, middle one or randomly any.
- Make array ideal according to that prime, i.e. add $D_i$ so that $(A_1*A_2..*A_N)\%P$ is maximum.
- Pray that this solution gets better points.
By roughly around 20-25 submissions, people experimented with what prime to take. Most of them settled on the median prime.
A good number of approaches used simulation and storing array and its result. Eg-
cin>>arr[i];
Store arr[i]+rand()%k;//Store in a vector etc.
Compute score for the just stored array.
Repeat above 250-400 times.
Print the configuration with maximum score
Depending on luck and number of simulation, the above approach fetched $88-94.7$ points. I saw quite a few with $94.7$ points.
Some of the top approaches also use the concept of simulating till just about to time-out. The contestants chosed a distribution (random, or some other) which they simulated for $\approx3.8-3.95$ seconds where they sought to see which choice of $D_i$ is increasing score for a particular $A_i$. When about to time out, they aborted the process and printed the output they got.
2. Div1
The performance of Div1 was kind of similar to Div2 xD. One of the codes which got $91.1$ points at pretest was-
cin>>A[i];
cout<< A[i]+K/2;
Most of the approaches were common- like simulation till best answer, or take $rand()$ values $300-400$ times. Omitting the common approaches, the approaches of top solutions were quite distinct. (However, most of them are hard to decipher due to 300+ lines of code).
Some crucial optimizations were, however, seen. For example, lets say I got some values of $D_1,D_2...D_N$ and calculated the value of $Score=(A_1+D_1)*(A_2+D_2)*...*(A_N+D_N)\%P_i$. The top solutions preferred to change $D_i$ one by one, and re-calculate $Score$ in $O(Log(A_i+D_i))$ by using inverses as - $NewScore=({A_i+D_{old}})^{-1}*Score*(A_i+D_{new})\%P_i$. This method got $95+$ points on pretest.
Some of the good top codes deserve a mention here. These codes are what one can call crisp :)
- Python Code by @gorre_morre
- C++ by @anoxx_23
- C++ by @mihaibunget
As usual, I want to invite everybody (yes, everybody, not just the top scorers) to discuss their approaches so that we can have an engaging and learning insights into various intuitions :)
CHEF VIJJU'S CORNER:
1. The very first solution submitted by tester to test this problem was also simply printing back the input xD. After that as many as $16$ more submissions were made.
2.Lets discuss the setter's approach here. Lets take a random subset (serveral times) of array $P[]$ and multiply the primes in this subset. Lets call their multiple $MUL$. Now, we now that $MUL\%P_i=0$ where $P_i$ is a prime in the subset.Now, our aim is to get the value of $(A_1+D_1)*(A_2+D_2)....*(A_N+D_N)$ closer to (preferably exactly equal to) $MUL-x$. This is because, by applying $\%$ operation for various $P_i$, we will be left with $MUL\%P_i-x\%P_i=(-x)\%P_i$. We can go greedily and try to factorize $MUL-1,MUL-2,...,MUL-x$ (The exact value of $x$ can be experimented upon). The factorization will help us in manipulation of $D_i$ values.
One thing to check is that, $(A_1+K)*(A_2+K)..*(A_N+K)$ must have a value more than $MUL$ else the above scenario may not be possible. We can check this by using $log$ function, i.e. by changing expression $(A_1+K)*(A_2+K)..*(A_N+K)$
to-
$Log(A_1+K)+Log(A_2+K)+...+Log(A_N+K)$.
Similarly, $MUL$ can be expressed as $(Log(P_1) +Log(P_2)+....+Log(P_N))$
You can find good practice problem here
3.There is also a better random generator in C++ known as Mersenne Twister or mt19937. It is available from C++11 and later. Some of the advantages it has over rand() are that-
- mt19937 has much longer period than that of rand. This means that it will take its random sequence much longer to repeat itself again.
- It much better statistical behavior.
- Several different random number generator engines can be initiated simultaneously with different seed, compared with the single “global” seed srand() provides
In Code Melange (Rated) contest problem, Xorangements problem giving WA to my solution
In Code Melange (Rated) contest problem, Xorangements giving WA to my solution
According to me, my Code is passing all test cases.. can anyOne give any test case in which my program is getting failed
and if anyOne come to know why my program getting failed, that reason will be bonus..
thanks in Advance
MULTQ3 - Editorial
PROBLEM LINKS
DIFFICULTY
MEDIUM
EXPLANATION
The problem can be solved using segment trees. Every node of the tree stores the following data :
1) tree0[k] : In the range [low..high] covered by this node, how many numbers are divisible by 3 considering just additions performed on numbers totally inside this range and not considering additions performed on ranges which are a subrange of the range covered at node k/2
2) tree1[k] : In the range [low..high] covered by this node, how many numbers leave a remainder of 1 when divided by 3 considering just additions performed on numbers totally inside this range and not considering additions performed on ranges which are a subrange of the range covered at node k/2
3) add[k] : What is the quantity which is added to all numbers totally inside this range and not considering additions performed on ranges which are a subrange of the range covered at node k/2
Why does Contest Ranking page not show the ranking of the users who scored 0 points?
Contest Ranking page does not show the ranking of the users who participated in the contest but not scored any point.
But, at the end of the contest, his/her ranking is shown on the user's profile page under Rating Graphs section.
I think, Contest Ranks page should show the ranking of each participating user whether he/she solved any problem or not, as it would help to predict the rating of a user if someone wants to develop rating predictor tool.
Because to predict the rating of a user, we need the information of other participating users in the contest.
So, its a request to add the ranking of each user who participated in the contest to the contest ranking page.
CLKLZM - Editorial
PROBLEM LINK:
Author and Editorialist:Soumik Sarkar
Tester:Sarthak Manna
DIFFICULTY:
EASY
PREREQUISITES:
Sorted set/Priority queue/Heap, Difference array
PROBLEM:
There is an array $Z$ of size $N$ denoting the health of $N$ zombies. There also $M$ types of beams of the form $(L, R, K)$ where $K$ denotes the number of times the beam can be used to decrease every element in $Z[L..R]$ by $1$. Find the minimum number of beam drops needed to reduce all elements in $Z$ to $0$ or determine if it is impossible.
EXPLANATION:
Consider the first zombie $Z[1]$. This zombie can only be affected by beams whose $L = 1$. Let's gather all such beams into a set $U$. If we want to reduce $Z[1]$ to $0$, we have to drop some beams from $U$. Of course we should drop the number of beams exactly equal to its health and not waste any beams. The question is.. which beams should we drop?
Here it makes sense to make a greedy choice and drop the beams from $U$ with largest $R$. That way we are affecting maximum zombies to the right of $L$ at the same time.
After killing the first zombie let us move to $Z[2]$. Of course $Z[2]$ may already have been reduced to $0$ after being affected by the beams that we used on $Z[1]$, but let us assume it is still non-zero. Now we are faced with a similar situation as before. Only those beams with $L \le 2$ can affect $Z[2]$. But all beams with $L = 1$ were added to $U$, and some of them are even already used. So we must add all the beams that have $L=2$ to the leftover beams in $U$, and make greedy choices again to reduce $Z[2]$.
Generalizing, the solution involves maintaining an active set of beams $U$. At any index $i$, all beams that can affect $i$, ie. beams that have $L \le i$, are either in set $U$ or have been used up. To kill zombie $i$, only as many beams as required are used, the beams with largest $R$ being used first. The process is carried out for $i = 1$ to $N$. The algorithm can be described as follows:
U = empty set
ans = 0
for i in [1..N]:
add all beams with L = i to U
while Z[i] > 0:
let b be the beam with largest R from U
if U is empty or b.R < i:
zombie i cannot be killed
exit loop
if b.K > Z[i]:
ans = ans + Z[i]
b.K = b.K - Z[i]
reduce every element in Z[i..b.R] by Z[i]
else:
ans = ans + b.K
Z[i] = Z[i] - b.K
reduce every element in Z[i..b.R] by b.K
remove b from U
The above strategy is optimal, but how can we implement it efficiently?
The two procedures that are non-trivial are retrieving the update with largest $R$ from $U$ and applying decrement operations on a range $Z[L..R]$.
For the first we can maintain $U$ as a sorted set or a priority queue. This allows retrieval of largest element in $\mathcal{O}(\log N)$ time. Most languages have implementations of these structures in the standard library.
For the second the simplest solution is to use a difference array D. Generally speaking, to apply an update on $[L..R]$ we perform D[L] += X and D[R + 1] -= X and then get the original array using prefix sums. Here we need to apply the updates as we go along. Note that the updates to be applied only affect elements to the right of the current index, so we can maintain the prefix sum in a variable and just modify D[R + 1]as required.
The complexity of the solution is $\mathcal{O}((N + M)\log M)$.
AUTHOR'S AND TESTER'S SOLUTION:
Author's solution can be found here
Tester's solution can be found here.
Can anyone help me with Chef and Chefcoin from February Cook-Off 2018 Contest?
Hello friends can someone tell me how to approach this problem ??
@vijju123@taran_1407@vivek_1998299@meooow@john_smith_3@aryanc403@vbt_95
Code Melange (Rated) contest editorial not published till now?
waiting For Codemelange (rated) contest Editorial... plz admin sir look at matter and upload as early as possible.. Waiting for editorials to understand some problem solution
NUMPY support
is numpy supported by codechef server????