Does time limit exceed means our answer was correct but time to run was more? I am getting time limit exceed error, Time to run shown as 1.01 seconds while under the question its shown as 1-2 seconds. Can someone explain?

http://www.codechef.com/status/PRPALIN

this is the link to my code....On my system it gives correct output for every input..I don't know against what input is it being tested..please help me....Otherwise give me some input cases or else check that yourself...but please do point out the mistakes..

include<stdio.h>

int main() {
float x,y;

scanf("%f %f",&x,&y);
if(((int)x%5==0) && (x + .5 <= y)) 
printf(".2f",y-x-.5);
else
printf(".2f",y);
return 0;

}

I was solving this question but I am getting WA. Can someone point where I am going wrong or any test case where i am getting WA Here is my link to the code.

include <stdio.h>

int main() { long long a[10000],b[100000]; long long d; for (d=0;d<=1000000000000000;d++) { scanf("%d", &a[d]); if (a[d] = 42) { break; } else { a[d] = b[d]; } } for (d=0;d<=10000000000000;d++) { if (b[d] = 0) { break; } else { printf("%d", &b[d]); }} return 0; }

PROBLEM LINK:

Contest
Practice

Setter-Arjun Arul_/\_
Tester-Arjun Arul_/\_ , Animesh Fatehpuria
Editorialist-Abhishek Pandey

DIFFICULTY:

MEDIUM-HARD

PRE-REQUISITES:

Mincut-Maxflow Algorithm (especially Cycle Cancelling Algorithm ), Bellman Ford Algorithm

These pre-requisites are the basic requirements which must be sufficed before proceeding next. Hence, make sure you have an idea about what above mentioned things are :).

PROBLEM:

For a directed graph of $N$ nodes, you can remove some edges. For each node, you must make outdegree-indegree=0. (i.e. Outdegree should be equal to indegree for each node.)

QUICK EXPLANATION:

The most important step to solve this problem is to identify it to be a min-cut max-flow problem. Once you do so, we will construct our graph in this fashion-

1. Since we can do nothing about vital edges, we note their effect on degree and discard them. We then take input about non-vital edges in similar fashion, but we dont discard them.
2. For each node with Outdegree>Indegree, we give an edge from source to that node with capacity= OutDegree-Indegree ,cost=0.
3. For each node with Indegree>Outdegree, we give an edge from that node to sink with capacity=Indegree-Outdegree, cost=0.
4. We make graph out of non-vital edges. Each such edge has cost=capacity=1.
5. Now we apply the standard min-cut max-flow algorithms, with maximum flow =(OutDegree+Indegree)/2 [Outdegree=Excess OutDegree, Indegree= Excess Indegree]
6. If maximum flow is achievable, we print the cost, which is edges cut, else we print -1.

EXPLANATION:

I first hope that you guys went through the pre-requisite links. If not, please do so, its not too late yet. :) . At any step, if you feel lost, or have any doubt related to implementation, please open editorialist's solution in another tab and have a look there as well :) .

The editorial is divided into following sections-

1. Identifying this is a MinCut-MaxFlow question
2. Constructing the Graph
3. Deriving answer from it

1. Identifying this is a MinCut-MaxFlow question-

The following points should guide you in identifying such questions-

1. Low constraints so that a $O(VE)$ or $O(V{E}^{2})$ &etc. algorithm passes.
2. Take "Excess Indegree/Outdegree" as required flow which must pass through a node, Combined with need of minimum cuts/removal of edges, we can see it as a MinCut-MaxFlow algorithm.

2. Constructing the Graph-

This section will take a good portion of editorial, as this part is not intuitive and hence deserves explanation.

a. Are Vital edges really vital for the solution?

First, we must analyze the input carefully. We see that the vital edges are not important to us. Why? To answer that, we must see what exactly are we taking as "flow". I took flow to be "edges cut in a path to satisfy Outdegree=Indegree relation" . In this sense, we can really not have a "flow" through vital edges as we cannot cut them. (The algorithm in our solution "cuts" the edges in path where flow is happening.) Hence, we do nothing but note the effect of vital edges on degree of nodes.

b. What about non-vital edges?

We can cut the non-vital edges. Each edge cut will reduce outdegree of one node and indegree of another by 1. Hence, cost and capacity of these edges should be $1$. We follow typical steps to make a graph from them.

c. What about source and sink?

We add our own $2$ nodes as Source and Sink. My solution follows 1-based indexing, hence I used Node 0 and Node (N+1) as source and sink respectively. We used the convention that nodes will have "Positive Outdegree and Negative Indegree" [Outgoing edges contribute +1, incoming contribute -1] . You can use your own convention, but make sure to change other things accordingly!

For each $Node$ $i$ with excess OutDegree, we add an edge from source to that $Node$ $i$, with cost=0 [Since this edge should not affect answer] and capacity= $|Excess Degree|$. For each $Node$ $i$ with excess indegree, we add an edge from that $Node$ $i$ to sink, with cost=0 and capacity= $|Excess Degree|$.

3. Deriving the answer from this graph-

Before proceeding further, make sure to be well versed with the reverse graph theory in the MinCut-MaxFlow link I provided.

a. When will answer exist?
Firstly, it should be intuitive that for a valid solution, Total amount of Excess Outdegree = Total Amount of Excess Indegree. If this is not the case, the answer is $-1$. Why is this happening though?

b. What is the value of MaxFlow?

Follow the reasoning above. Since all we are doing is directing flow from "excess to deficit". (A very good analogy is to take Excess Outdegree nodes having positive potential, Excess Indegree nodes with negative potential, and flow as current.)

Each edge has capacity 1, will satisfy outdegree of one node and indegree of another. Hence the required flow will be Flow=(|Excess Outdegree|+|Excess Indegree|)/2 .

Q- Can you use my inference in part a. to simply the above equation?

c. What do we actually do?

We need to have flow in our network equal to maxflow. If this cannot be achieved, then the answer does not exist. Recall from the reverse graph section of pre-requisites, that in condition of maxflow, source will not be connected to sink. (In real graph terms, it means there is no path with flow capacity>0 connecting sink and source. i.e. all paths are being used to their fullest). We will use this later.

While we dont get our flow equal to required maxflow , we find an augmenting path from source to sink and allow "flow" through the path. (i.e. we deduct flow-occuring through path from capacity of each involved edge) and compute cost. If we can reach the maxflow, we break out and give the current cost (i.e. edges cut) as the answer.

But...What if we cannot find a path from source to sink?

(Answer is in tab below, try to answer on your own first).

Once we get final flow through the network, and the cost, we can easily see what the answer is.

SOLUTION:

Editorialist's

CHEF VIJJU'S CORNER:

1.We used Bellman Ford because of possible negative weight (cost) in edges. Can we use Dijkstra's algorithm here? Some people used both! "If no negative edge, use Dijkstra, else Bellman Ford".
2.A very common question is "For graphs with negative edges, we just add a positive constant $K$ to all weights and apply Dijkstra and then subtract similarly from answer." . Is this procedure correct? How does it interact with the negative cycle anomaly in such graphs?
3.Is Dijkstra completely inapplicable to all graphs with any negative weight edges?
4.After going through editorialist's solution, how many of you want to kill and burn him on a stake for not making a function/constructor to make/add edges? :p

PROBLEM LINK:

Contest(Mirror)
Practice

Setter-
Tester-Kevin Charles Atienza
Editorialist-Abhishek Pandey

DIFFICULTY:

MEDIUM-HARD

PRE-REQUISITES:

2-D Arrays and Strings, Probability and Expected Values, C.O.B.F. Strategy, Binary Search ,BFS on a Matrix (optional) , Pre-Processing

PROBLEM:

Given a 2-D character grid, representing color of painted houses (or if the house is not painted), we need to find the expected beauty of the city, beauty being defined as "The overall beauty of the town will be equal to the total number of beautiful square sub-grids (continuous) in the town."

QUICK EXPLANATION:

This problem, although looks complex, is actually fairly simply. The chief idea of the solution is pre-processing to reduce complexity. What observations, or pre-processing can you make to optimize your brute force significantly better time complexity. One of the chief observations is that beauty depends on number of sub-grids and not on size of sub-grids. Hence, contribution of sub-grids with large unpainted houses is negligible! (A completely unpainted sub-grid with 100 houses contributes ${3}^{-100}$ to the answer!!). The tester used a combination of above along with Binary Search and some formulas to bring down complexity to $O(NMLogL)$ where $L$ is the length of subgrid.

EXPLANATION:

This question is a deceptively simple question once you decide and plan on what to do. A Clever Optimization of Brute Force (C.O.B.F.) is needed here. The editorial is divided into several parts-

1. Calculating contribution of a subgrid filled with houses of same color.
2. Contribution of unpainted houses and when to discard it
3. How to optimize it.

1. Calculating contribution of a subgrid filled with houses of same colors-

Lets say, we have a sub-grid like-

RRR RRR RRR

What is the contribution of this sub-grid to beauty? Now, there are two ways to approach this problem.

First is, we can go by the mathematical approach. We say that there are $(3-0)*(3-0)$ squares of size $1$, then $(3-1)*(3-1)$ squares of size $2$ and $(3-2)*(3-2)$ squares of size $3$. By some mathematics, we can see that the answer is $\sum_{l=0}^{min(n,m)-1} (n-l)*(m-l)$. You can try deriving it (derivation in Chef Vijju's Corner given for reference).

Theres, however, another method which I want to explain. The one which we will be using. This method is nothing but a simply brute force. What we will do is-

1. For each house $(i,j)$, do following-
2. For each possible length $L$ from $L=1$ to $Length$ $of$ $subgrid$, do 3.
3. Check if a valid square of length $L$ is possible starting from that cell $(i,j)$. If yes, add $1$ to answer, else break and start checking another cell.

Basically what the above will do, it will chose a cell. Then it will check if a square of length $1$ is possible starting from it. Then it will check if a square of length $2$ is possible from it. So on and so forth, it will check if a square of length, say $l$ is possible or not. If possible, it will add $1$ to answer and check for $l+1$, else it will break out and check the next cell. This will also give the same answer.

But of course, this brute force approach will time out. Also, we haven't considered anything about unpainted houses yet! What about that? Any thoughts of what change the unpainted houses will bring to the picture?

2. Contribution of unpainted houses and when to discard it-

There can be three cases here.

1. We get a sub grid where all houses are unpainted.
2. We get a sub grid where some houses are unpainted, and its possible to convert this sub-grid into a sub-grid where "All houses are of same color" by appropriately painting unpainted houses.
3. We cannot get all houses in sub-grid of same color no matter what (because of some conflicting colors of houses which are already painted).

By first section, it would be clear that we are leaning towards sub-grids of type $1$ and $2$ for optimization of brute force. The reason for this is simple, in a sub-grid of type $1$ or $2$, we dont have to check if the sub-grid is valid to be made beautiful or not, as its guaranteed by definition.

Also, notice that, we can decompose sub-grid of type $3$ as "Its made up of various subgrids of type $1$ and $2$ (even if the size of these sub-grid is 1!!)". An example is given in tab for those in confusion.

Now, what about the contribution when houses are unpainted? Lets take an example of sub-grid-

RRR R*R RR*

Lets dry-run our brute force algorithm here.

We start at cell $(1,1)$ ($1-based$ indexing). We check if a square of size $1$ is possible or not. It is, we add $1$ to answer.

We now check if a square of size $2$ is possible or not. It is, if the unpainted house at $(2,2)$ is painted red. What is the probability that the house will be painted red? Of course, its $P(Red)=\frac{1}{3}$, as we have 3 colors, out of which any one can be chosen with equal probability. Recall that Expected value $E(x)=P(X)*X$. $P(X)=\frac{1}{3}$ as we calculated above. Also, if we paint the house red, we get 1 more beautiful sub-grid which adds $1$ to the beauty (strictly w.r.t. when starting cell is $(1,1).$) Hence, we add $E(x)=\frac{1}{3}*1=\frac{1}{3}$ to the answer.

Then, we will check for a square of size $3$ starting from $(1,1)$ now. It is possible as well, if both the unpainted houses are painted red. The probability of this is $P(Red)=\frac{1}{9}$, and hence we add $\frac{1}{9}*1=\frac{1}{9}$ to the answer.

No more squares are possible which start from $(1,1)$, hence we now move on to cell $(2,1)$ and repeat the above process again.

Notice how each unpainted house divided the contribution by $3$. Say we are checking a square grid of $L=100$ which has $80$ unpainted houses. It will add ${3}^{-80}$ to the final answer. Clearly, such a small value wont affect our final result as an absolute difference of ${10}^{-2}$ is allowed. Also, such calculations take up lot of time. Hence, we decide that if the number of unpainted houses becomes more than $50$, we disregard any further contributions and move on to next cell.

Note that, by above example, we can clearly see that if there are $k$ unpainted houses in the square grid under consideration, then we add ${3}^{-k}$ to the contribution.

This was dealing with sub-grids of type $2$. Dealing with sub-grids of type $1$ is even easier!

Say we have got-

***
***
***

Lets apply our brute force here.

Starting from $(1,1)$ again, we check if a beautiful sub-grid of size $1$ is possible. It is, if the unpainted house is painted $R$ , $B$ or $G$. Each color has a probability of $\frac{1}{3}$. But this time, we have $3$ valid choices instead of just one (as house can be painted either Red, or Blue, or Green instead of only 1 color which happened in case above!). Hence, we will add $E(x)=3*\frac{1}{3}=1$ to the answer.

Now we check if a subgrid of size $2$ is possible, which starts from $(1,1)$. It is, if all $4$ houses are painted $R$,$B$ or $G$. Hence, we add $E(x)=3*\frac{1}{{3}^{4}}$ to the answer. (Observe that we have to paint ALL houses either Red, or Blue, or Green. Hence, only $3$ valid options).

For size $3$, I think you guys can handle yourself now.

So far, we saw how brute force works, and got the essence of the solution. But, how to optimize the brute force? We got one point, that we should stop calculation if number of unpainted houses becomes too large. Any other?

3. How to optimize it-

We are doing better than original brute force by stopping if number of unpainted houses is too large. But we need something more. Note that a lot of time is consumed in the step "Check if square grid of length $1$ is possible, Check if square grid of length $2$ is possible, $...$"

Lets see the sub-grid example of-

RRRRRR RRRRRR RRRRRR RRR*RR RRRRRR RRRRRR

Since there are no unpainted houses in between square grid of size $1$ to size $3$ which start from cell $(1,1)$, we already know we will be getting a contribution of $3$ in final answer. No need to check for square grid of any other length in between. For square grid of size $4$, we know the contribution to expected value is $\frac{1}{3}$, and its same for square grids of size $5$ and $6$ as well, no need to check individually.

How to prevent the individual checking?

One thing we can do is, to first, find largest length of subgrid of type $1$ and type $2$ which start from the cell under consideration, $(i,j)$. We can do so quickly by Binary Search and some pre-processed data. We can store a prefix sum in a $2-D$ prefix sum array (refer to counts[k][i][j] editorialist's solution) and use it to tell if the entire sub-grid starting from $(i,j)$ consists of houses of only single color (and unpainted houses) only or not. With this, we know the valid sub-grid size.

With some similar pre-processing, we also store the location of next unpainted house from $(i,j)$(refer to nextLeft[i][j] and nextUp[i][j] in Editorialist's solution). This helps because we can skip checking squares whose sizes "lie in-between" as explained in above example. This step's validity can be proved. We know that, contribution of a grid depends on number of unpainted houses in it. If count of unpainted house of two square grids are same, then their contribution is same as well.

We combine the above with our very first observation, to discontinue counting contribution if number of unpainted house becomes too large. Lets say that we fixed this number to $50$. Calculate the time complexity now-

$Time$ $Complexity-$ $O(NM *LogL*50)\equiv O(NMLogL)$ in worst case, which can easily pass. Note that range of L is $0\le L \le min(n,m)$.

SOLUTION

Editorialist

I had purposefully not gone deep into implementation. The editorial would had else, become very long. If you got the logic and intuition, then go ahead and look at the editorialist's solution. I have commented things so that its easier to understand implementation :)

CHEF VIJJU'S CORNER:

1. This question, uptil now, has no $AC$ solution in practice....Editorialist's of course! xD

2. Make sure you use long double instead of double data type for better precision. I found double data type giving undue WA's , so watch out!

3. Derivation of $\sum_{l=0}^{min(n,m)-1} (n-l)*(m-l)$

Any request for explanations, examples, derivations etc. are welcome. I would be grateful if the community can suggest related problems, I had a hard time finding a good one :(.

PROBLEM LINK:

Contest
Practice

Setter-
Tester-
Editorialist-Abhishek Pandey

DIFFICULTY:

Easy

PRE-REQUISITES:

Arrays, Looping, Logical thinking.

PROBLEM:

Formally, the problem can be put up as, you have to re-arrange a sequence of $N$ numbers from $[1,N]$, such that-

1. The number at index $S$ is $Q$.
2. The maximum absolute difference between adjacent numbers is minimum,i.e. "minimize the maximum absolute difference".

We need to print any such sequence satisfying the above along with the maximum absolute difference.

QUICK EXPLANTION:

After some examples, we see that we can always get a difference of 2 is possible. We can easily check if a difference of 1 is possible or not. If a difference of 1 is not possible, then the we can always minimize the "maximum absolute difference" to 2. This is done by printing numbers at difference of 2 (or 1 if needed), starting from index $S$. Take special care for $N=1$ case where the difference is 0!!

EXPLANTION:

The question in itself is pretty much straightforward. The editorial is divided into 3 sections, 1 each for each possible answer.

(Henceforth, I will refer to "minimized maximum absolute difference" as "answer". Please dont get confused with the terminology.)

Cases when ans=0:

This is possible only for $N=1$ case, and is a special case which should be handled manually.

Cases where ans=1:

We can trivially see when its possible for the "maximum absolute difference" to be equal to 1. This happens if, and only if, the series is of either of the 2 forms-

1. $1,2,3...N$
2. $N,N-1,N-2....3,2,1$

The first series is possible if and only if $(S==Q)$ , while the other series is possible iff $[Q==(N+1-S)]$.

Again, we can deal with this case manually and print the respective series for which the condition is satisfied.

When ans=2:

Now this is the heart of the question. There are 2 things that we must deal here-

1. Proving that answer of 2 is possible (and answer greater than 2 are not.)
2. Constructing the series (We will discuss 2 methods here)

We dealt with cases of $N=0$ and $N=1$. Intuitively, the number to consider is 2. Now, how to get an idea that answer of 2 is possible, and that its not anything else (like, $logN$ for example). Fortunately, is a method to support (or develop) or intuition.

Write a brute force which checks all the permutations possible, and among the ones satisfying the conditions (The element at index $S$ must $Q$), finds sequences with minimum answer and print them. There on you might catch the pattern there, and observe that answer doesnt grow with $N$, but stays at a constant $2$, even for $N=10,11..etc$. This is the most standard method to do so. You can use STL to help you here as well (Read Chef Vijju's corner).

A kind of informal proof will go on lines, that, numbers of same parity can be grouped together such that the endpoints (where they are "adjacent" to even numbers) are 1 and $N-1$ (assuming N is even). Now we can place $N$, and $2$ at endpoints of even numbers, and arrange remaining $N/2$ numbers in form $2,4,6...N$. For example, we can always form permutations of this kind by swapping-

$N=8,S=3,Q=5$ - [1,3,5,7,8,6,4,2]

$N=8,S=4,Q=5$ - [2,1,3,5,7,8,6,4] (here odd segment is "sandwiched" b/w 2 even ones).

Notice how the 2nd case is nothing but a "cyclic shift" of the above array. We can similarly cyclically shift the array till and until we get $arr[S]=Q$.

This is the first method of construction.

Second Method

Obviously, there are only 2 cases where $ans=1$ is possible, and only 1 with $ans=0$. Using some manipulations on smaller values of $N$, you can easily test for $N=2$ using this trick- First assign $arr[S]=Q$. Now assign $arr[S+1]=Q+2$, $arr[S+2]=Q+4$ &etc. and $arr[S-1]=Q-2$ , $arr[S-2]=Q-4$...and so on. If at any instance, $S+i$ crosses $N$ or $0$, stop the series there. If at any instance,$Q+2i$ exceeds $N$, then change pattern- start using numbers from $(N-1),(N-3)...$. Similar case if $(N-2i)$ drops below $1$.

Dont worry, it seems confusing at first, but it will be clear with an example.

Lets say, our input is $N=10, S=5 Q=7$

Now-

1. First, arr[S]=Q. So our array is $[0,0,0,0,7,0,0,0,0,0]$
2. Lets start from right, and assign Q+2,Q+4 etc. (till we can) to subsequent indices. Our new array becomes $[0,0,0,0,7,9,0,0,0,0]$.
3. We see that we couldnt assign anything after $9$ as next term is more than $N(=10)$. Now, we change pattern. The next term after highest possible odd will be highest possible even, which in this case is 10. New array= $[0,0,0,0,7,9,10,0,0,0]$.
4. Again fill elements in right at a difference of 2. New array is $[0,0,0,0,7,9,10,8,6,4]$. We now reached the end here.
5. Start filling left elements now, by Q-2,Q-4...etc, as far as we can. New array becomes $[0,1,3,5,7,9,10,8,6,4]$
6. We cannot fill any more with odd terms and next term will be less than 0. Again, change pattern. Lowest odd should be followed by lowest even, which is 2. New array=$[2,1,3,5,7,9,10,8,6,4]$

We are done. Feel free to try some of your own experiments here!!.

SOLUTION:

Editorialist's Solution- Pattern
Editorialist's Solution- Cyclic Shift

$TimeComplexity=O(N)$
$SpaceComplexity=O(N)$

CHEF VIJJU'S CORNER:

1.Let me take the chance to introduce you to next_permutation() function of C++ STL. It saves you a lot of time in writing code where you have to generate all permutations. The brute force can be simplified to a great deal with this function. Also, if you;re a regular guy giving short contests at Codeforces etc. , then this function will come in handy quite many times.

2.The basic question in everybody's mind is "How to approach constructive algorithm questions." Honestly, I think the answer depends. The setter thought of something, noticed a pattern and framed the question. Going by different directions can, sometimes make problem really trivial, or complicate it to a great deal. I will say it again comes with practice. At least for me, I first solved the problem using brute force, observation and pattern making. Its after getting AC (and while writing this editorial), that the cyclic shift technique came in my mind. So, yes, just practice and keep your mind sharp. Thats the best advise anyone can give.

PROBLEM LINK:

Contest
Practice

Setter-
Tester- Multiple
Editorialist-Abhishek Pandey

DIFFICULTY:

Medium

PRE-REQUISITES:

Geometry, Point Inside a Polygon Algorithms , Distance formula, Math, Conditionals.

Knowing about vectors and cross product will help in understanding Point inside a Polygon algorithms, and is hence advised.

DO NOT USE THE ALGORITHM GIVEN AT GEEKS FOR GEEKS FOR POINT INSIDE POLYGON- ITS INCORRECT AND FAILS AT EDGE CASES!!

PROBLEM:

You are asked to find the shortest distance between 2 points such that it does not cross the given quadrilateral. In case no answer exists, print $-1$.

QUICK EXPLANATION:

We first find out if an answer is possible or not by using Point inside a polygon algorithms, such as Crossing Number and Winding Number (refer to the link in pre-requisites). Once we know an answer is possible, its all about conditionals. Alternatively, we can use dp to ease out and avoid those tedious cases!

EXPLANATION:

Depending on your approach and carefulness in implementation, this problem can either by an easy point or spawn of the devil itself. Usually, when such kind of questions are faced, its better to sit back and think first. Think on what tools or functions you might need, what operations you would be performing. Like, we will be calculating distances between points a LOT in this problem. It isnt advised to write the formula everywhere you use that. You have more chances of committing error that way. Make a clean function of it, and use it whenever you need. These type of questions dont take long to get really messy if you dont follow proper programming approach and practice.

Now, coming to the question, we can clearly see that the answer will either exist or be -1. ("Great revelation you made @vijju123 "- lol). Coming to the editorial, it is divided into 2 sections, one for each part. :)

When no answer exist-

This clearly happens when one of them is inside the castle, while other is outside it. This is also one of the easier - but trickier section to code.

Now, finding if a point is inside a polygon or not, is a standard question, with well known algorithms. There are 2 tools to determine if a point is inside a polygon or not- Winding Number and Crossing Number. You can read about them in the link given- its no use doing repetitions in an editorial.

Now, I'd suggest to always use winding number, because of 2 cases-

• Crossing Number has some corner cases. Say your horizontal line crosses polygon at edge. Its intersection is counted twice instead of once, since each vertex is a part of 2 edges. (So if we dont handle this manually, we will add 2 to answer instead of 1). Lets say you handled this case, then theres another case where both points are outside, and the line joining them just touches a vertex. Another case too handle :) . So on and so forth you can find ample of problems in this approach.
• Crossing number holds no good if polygon is twisted, i.e. edges intersect with each other. Winding number works there.

Winding number's implementation can be seen in the link, and in the editorialist's solution.

For those who want to use crossing number, there are 2 ways to relieve yourself of these case handling.

One is, you find out point of intersection. In crossing number, we see intersection of the horizontal ray (from point to be tested) with edges. We know equation of both lines. We also know the y co-ordinate, since ray is horizontal and we know the point to be tested. Find out the x co-ordinate now. See if this intersection happens on edge or not. Make sure you count each point only once. HORIZONTAL EDGES MUST BE EXEMPTED FROM CROSSING NUMBER TEST!

Another one used by testers is highly innovative and impressive. What they did, is that instead of taking a strict horizontal ray, they took an "Almost horizontal ray". i.e., the ray starts from $P$ , say $(x,y)$ and ends at $(x+{10}^{6},y+1)$. This ray, cannot be collinear with any point of the input, due to constraint of point being integers and extremely low slope of this ray. But the line intersection part is unaffected by it. This gets rid of all those corner cases like - line touching vertex, line intersecting vertex etc.

When answer exists-

Now, this part is pretty straight-forward, but really straining. There are two ways to approach this part.

The standard solution is of course, making cases. You can make cases on these lines-

1. When Jared can go straight to Payton
2. When Jared has to move across 1 vertex to go to payton. (Goto $Vertex$ $A$ and from there to Payton)
3. When Jared has to move across 2 vertices (From his original position to $Vertex$ $A$ and from there to $Vertex$ $B$ and from there to Payton).
4. When Jared has to move across 3 vertices.

Case 1 and 2 are pretty easy.

In case 3, you need to make sure of order, and if he can go to diagonally opposite vertex in straight path or not (This is done by checking if Jared and mid point [or any point] of this diagonal, both lie completely inside or completely outside). Further, you must check for direction. Meaning, if he visits vertex 1, he can either goto vertex 2 and then to payton, or goto vertex 4 and then to payton. Dont miss these cases!

Case 4 is by far quite complex. Since we are visiting 3 vertices, you can prove that you dont need to check for diagonals (visiting 3rd vertex will be, else, redundant). Just take care of order. That is, check for both paths $(Jared,1,2,3,Payton)$ and $(Jared,1,4,3,payton)$.

This was the first approach. Another approach used by tester, which is quite elegant, is to use dynamic programming.

First he took all 6 points in an array. The points were as - (Jared, 4 points of quadrilateral, Payton)

Then he made a 2-D array $d$$p$$[$$6$$]$$[$$6$$]$ , where $d$$p$$[$$i$$]$$[$$j$$]$ represents "Shortest distance from i to j". First, he calculated the distance between adjacent edges (i.e. $dp$$[$$i$$]$$[$$i$$\%4$$+1]$). Then he checked if its possible to visit diagonally opposite vertex or not. $dp[i][i]$ is, as usual, 0.

Once this was done, he looped through all 6 points **(Jared, 4 points of quadrilateral, Payton)** as-

for all points from  i=0 to 6:
   for all points from j=i+1 to 6
       if(either point i or point j are Jared or Payton)
           bool canGoStraight=true;
           for all k=points of polygon
                if point i,j,k and (k+1)%4 are all distinct, and line between i and j intersects edge
                between k and (k+1)%4
                            canGoStraight=false;
      if(canGoStraight==true)
           dp[i][j]=d[j][i]=Straight distance b/w i and j;

Now the only thing left is to see for cases where its not possible to go straight, i.e. we must visit at least one intermediate point/vertex to goto Payton.

He took care of it as-

     for(int k=0;k<6;k++)
           { //Let k be the intermediate point.
               for(i=0;i<6;i++)
               {
                   for(j=0;j<6;j++)
                   {
                       dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);
                       //If no straight path from i to j exists, then considering if we can 
                       //visit any intermediate point k to reach there.
                   }
               }
           }

Be careful though! The outer-most loop $must$ be that of k! If it is not, then you wont compute dp table properly. In this implementation, you are checking all points, as in, whether its possible to move from this vertex to another in shorter way, or of jared moving to vertex i in a shorter way etc. Obviously, its performing more than, say 200 operations to determine final answer.

If k is not the outermost loop, say you made it the innermost loop, then after mere 30 iterations you will come to condition-

for(i=0;i<6;i++)
  for(j=0;j<6;j++) //j is now 5.

But point 0 and point 5 are Jared and Payton- you are calculating the answer first and then updating the dp table correctly, which obviously leads to wrong answer!

SOLUTION:

Solution 1 -Based on dp approach of tester
Solution 2- Based on Conditionals - Refer to implementation of winding number, and crossing number here.

Chef Vijju's Corner :D

1.Some people feel that geometry problems are really tough. YES THEY ARE SOO RIGHT!! (Lol joke). But honestly, on a serious note, geometry problems need a good programming habit. You have almost infinite corner cases. You need to know the theorems, and you will have to write functions- because performing those mundane operations like finding distance between 2 points repeatedly is tedious. Again, not all are tough in implementing, but all have one edge case or the other.

2.How would you extend this problem for $N-sided$ $Polygon$? I think the tester's code can be modified a bit to give answer for this, because making conditionals gets exponentially tedious as number of vertices increase. Can you come up with the solution for this?

3.The tester (i.e @errichto i.e Kamil ) did this question in mere 90 lines!! Though I should not say 90, since many of the statements were clumped together in 1 line and some parts of the code were messy. Also, it had almost nil comments for the poor editorialist who has to understand what he did -_- . But on a serious note, its very rare to come across somebody who writes this clean code. In case you want to see - here is his solution. It was really pleasant to read that code, and there are lots of nice tricks which he used. Some of them were damn innovative, hats off to that.

my humble request to @admin to share test cases of contest problems with editorial, or provide feature to see test cases during submission after contest gets over..
while practicing one get WA, TLE or whatever error it must show testCases where code is failing similar to codeforces, hackerRank, hackerEarth etc. plateforms..

Reason is simple, during practice, when we try to upsolve contest problem, it will save our time to figure out what's wrong with our code
whenever we gets WA, then we try our best to figure out corner cases where code is failing, if succeed than its good
but if do not gets succeed than we post link to our submission on discuss, and we have to wait someOne will tell us corner case... most of times on codechef Discuss forum, someOne helps to figure out in which test case code is failing but someTimes we do not get replies...
if we know test cases, then we can figure out by ourselves where code is failing... and it will save our time to post "find where code is failing" type question on discuss and will also save others time of answering those questions..

i am facing this issue to figure out whats wrong with my june long challenge "TWOFL" problem
sorry for by bad English..

problem link:- link text

solution link:-link text

Test case (unlocked) link:-link text

Updated

My solution works fine on my pc command prompt. I debugged using test case gives output. But for hackerrank judge gives segmentation fault. Can someone plz tell what is making memory leak.

I attempted BEERUS with this approach, please tell me if this approach is wrong and how should i attempt it.

Using the property A|B + A&B = A+B , I store the sum of input array elements into array t;

Now each element of t is $ t[i] = (\sum_{i=1}^{n} node_i) + n.node_i$

Thus at $ sum = \sum_i^n t_i = n(\sum_{i=1}^{n} node_i)+ n(node_1 + node_2 + ... ) = 2n(\sum_{i=1}^{n} node_i) $

Therefore $ (\sum_{i=1}^{n} node_i) = sum/2n $

Which makes $ node_i = (t[i]-sum/2n)/n $

Now we have to find the maximum spanning tree. Since the weight of an edge is A&B + A|B = A+B

Therefore maximum path will be to go $max(node)->secondmax(node)$ and so on

Hence I found of maximum spanning tree to be $(2\sum_i^nnode_i) - min(node) - max(node)$

Thank you

Problem Link

Practice

Contest

Author:Rahim Mammadli

Tester:Misha Chorniy

Editorialist:Bhuvnesh Jain

Difficulty

EASY-MEDIUM

Prerequisites

Cross Product, Binary Search

Problem

Given a stationary point $P$ and a point $Q$ moving in straight line, indicate the time when $Q$ is visible from $P$, given that there am opaque sphere between them.

Explanation

We will try to find the solution in 2-D and then extend the idea to 3-D as well.

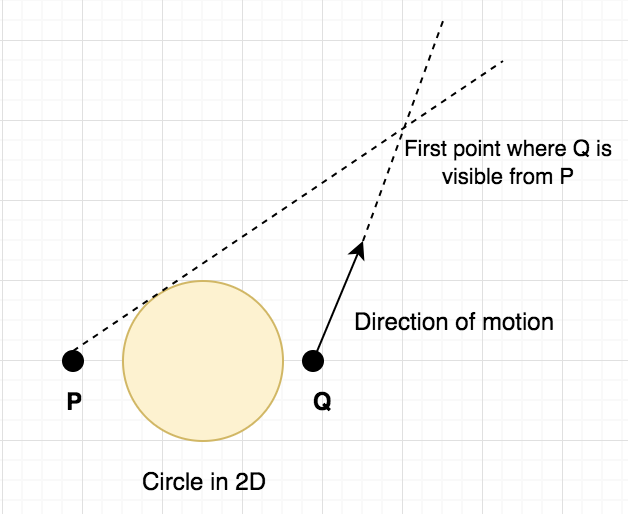
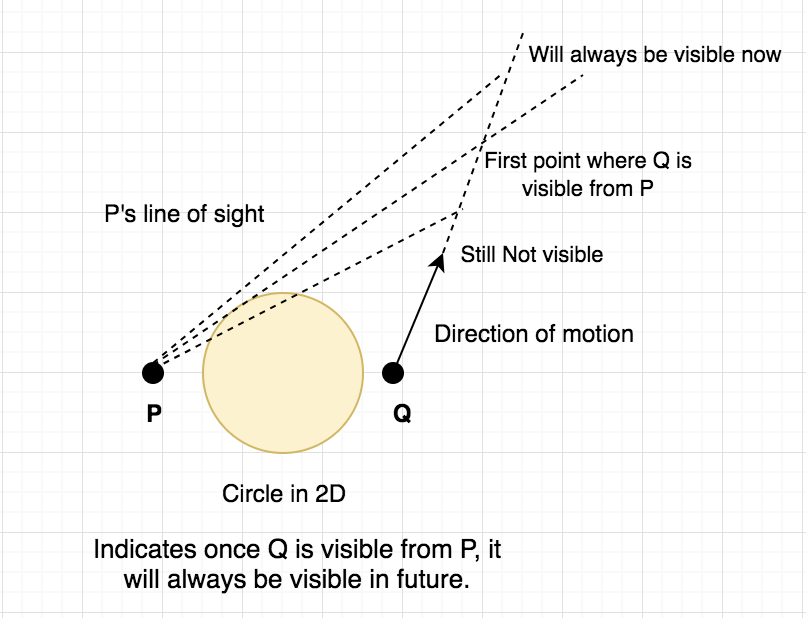
From the above figure, the first idea which can be clearly concluded is that, once point $Q$ becomes visible from $P$, it will remain visible forever. Before that, it will always remain invisible. This, the function (whether $Q$ is visible $P$ at given time $t$) follows the idea that it is false initially and after a certain point, it always remains true. This hints that we can binary search on the answer and just need to check whether the point $Q$ is visible from $P$ at given time $t$ or not. For more ideas on "Binary search" on such type of problem, refer to this awesome tutorial on topcoder. Hence, solution template looks like:

    double low = 0, high = 10^18
    for i in [1, 100]:
        double mid = (low + high) / 2
        if visible(P, Q, C, r, mid):
            high = mid
        else:
            low = mid
    double ans = (low + high) / 2

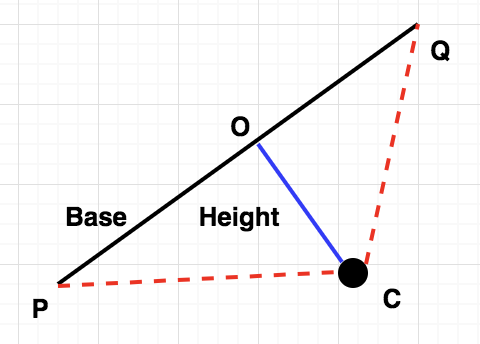
So, given a particular time $t$, we can first calculate the position of point $Q$. Join $P$ and $Q$ by a straight line. If the line doesn't pass through the circle, the point $Q$ is visible from $P$ else it is not visible. To check if a given line passes through the circle or not, it is enough to check that the perpendicular distance of the line from the centre, $C$, of the circle is greater than the radius, $r$, of the circle. For this, we first complete the triangle $PCQ$ and let the perpendicular distance of $PQ$ from $C$ be denoted by $CO$. Using the formula,

$$\text{Area of triangle} = \frac{1}{2} * \text{Base} * \text{Height} = \frac{1}{2} * CO * PQ$$

Since the area of the triangle can be found given 3 points in 2-D, and $PQ$ is the Euclidean distance between $P$ and $Q$, we can find the value of $CO$ efficiently. Finally, we just need to compare it to $r$, the radius of the circle.

For extending the solution in 3-D, the idea is same and we just need to find the area of a triangle in 3-D. For details, one can refer here. It can be clearly seen that the above formula holds for the 2-D case as well.

$$\text{Area of triangle in 2/3-D} = \frac{|CP X CQ|}{2}$$

where $CP$ and $CQ$ are vectors, $a X b$ denotes cross product of vectors and $|a|$ denotes the magnitude of vector.

Thus, to find the length of $CO$, we have

$$|CO| = \frac{2 * \text{Area of triangle PCQ}}{|PQ|} = \frac{|CP X CQ|}{|PQ|}$$

For more details, you may refer to the editorialist solution which exactly follows the above idea.

Extra Ideas/Caveats

The binary search implementation mentioned in the editorial is different from the one mentioned in Topcoder tutorial. Though both will give AC here, the one in Topcoder needs one to correctly set the Epsilon value for termination condition and sometimes can lead to wrong answers due to precision issues. The editorialist just prefers the above style to implement binary and ternary search involving doubles as calculation of epsilon is not required.

Note from the author

Finding the distance of a point from a line in 3-D is a generally common problem and also contains some edge cases where the point may not lie within the line segment region. But given the constraints of the problems, there are no edge cases but we should be aware of it in general.

Feel free to share your approach, if it was somewhat different.

Time Complexity

$O(1)$ per test case (around 100 iterations for binary search).

Space Complexity

$O(1)$

AUTHOR'S AND TESTER'S SOLUTIONS:

Author's solution can be found here.

Tester's solution can be found here.

Editorialist's solution can be found here.

I am currently using the syllabus of certification to prepare for coding interview, and then solving some more based on the category plus leetcode problems, is this a good way to prepare for directi interview? Thank you!

Can someone have a look at my code and tell why it is giving tle in last test case.

Question is :Chef And Fibonacci Array

Solution

Thanks in advance!

So due to some small mistake a while ago when my rating was dropped by around 500 points for plagiarism in a really old contest, I didnt say anything. I gave the June Long Challenge and to my surprise, despite having 500 points and a ranking of 71, I got an increase of just 200 points, while some other people of my college, some having solved only 2 questions got a boost of 175 points. Is there any basis behind this? What's the point of a lower rated person even solving the questions in long challenges then? Someone please look into this as I am not the only one pissed off by this.

PROBLEM LINK:

Practice
Contest

Author:Kamil Debowski
Primary Tester:Marek Sokołowski
Secondary Tester:Praveen Dhinwa
Editorialist:Praveen Dhinwa

DIFFICULTY:

cakewalk

PREREQUISITES:

none, knowledge of for or while loops in any programming language

PROBLEM:

Limak and Bob are friends who play a game involving eating candies. They take turns alternately with Limak starting first. Initially Limak eats 1 candy, then Bob eats 2 candies, then Limak 3 followed by Bob eating 4 candies and so on. Limak can eat at most $A$ candies, whereas Bob can eat at most $B$ candies. The person who is not able to eat the required candies in his turn will lose the game. Find out the winner of the game.

Problem constraints mention that $A$ and $B$ can be at max 1000. The idea of the solution is to implement the turns of the game. We iterate over the number of candies being eaten in the current starting from 1 onwards and check whether the current player can eat the desired amount of candies or not. We can find the current player by checking the parity of number of candies in the turn being eaten. You can see that Limak always eats odd number of candies, while Bob even number of candies. If the current player is not able to eat the required amount of candies, he will lose. Pseudo code follows.

limakCandies = 0 // denotes number of candies eaten by Limak.
bobCandies = 0 // denotes number of candies eaten by Bob.
c = 1;
while (true)
    // In this turn the person should eat exactly c candies.
    // if c is odd, then it is Limak's turn, otherwise Bob's.
    if c % 2 == 1:
        limakCandies += c;
        if (limakCandies > A):
            // limak can't eat these c candies, so Bob will win.
            winner = "Bob";
            break;
    else:
        bobCandies += c;
        if (bobCandies > B):
            // Bob can't eat these c candies, so Limak will win.
            winner = "Limak";
            break;

    c += 1;

Notice that the while loop can have at most $A + B$ iterations, i.e. at most $2000$ iterations. There are 1000 test cases. So, total number of operations will be around 2000 * 1000 = 2 * 10^6 which is sufficient to pass under a sec. For a rough guideline, you can assume that around $10^8$ operations take a second to execute. Please note that this is a rough guideline, actual number of operations depend very much on the implementation of the solution and also on the architecture of the machine on which your code is being judged. You should also account for the extra constant factor due to your implementation.

In fact, if you analyze carefully, you can prove that number of iterations of the while loop will much less than 2000, they will be around $\sqrt{2000}$, around 45. This is because we are subtracting $c$ candies each time, $c$ going from 1 to 2 to 3 and so on. As we know that sum of $1 + 2 + \dots + n = \frac{n \cdot (n+1)}{2} = \mathcal{O}(n^2)$. Therefore, $c$ will become greater than $A$ or $B$ in around $\sqrt{A + B}$ operations.

AUTHOR'S AND TESTER'S SOLUTIONS:

Setter
Tester1
Tester2

When and how will codechef contact college toppers who will be offered 100% scholarship for CCDSAP. And, also since I landed under top 20 Indians when will I get my laddus.

I know that I should keep patience but Since it is my first time, when I will get laddus, I am little excited about this.

Can someone please tell me where I am wrong . Here is my code. I maintained 2 segment trees for maximum query and for sum query and then I found lower bound of prefix sum for the interval where my sum/2 lies . Please someone reply :( what is the error in my code

PROBLEM LINK:

Practice
Contest

Author:Hasan Jaddouh
Primary Tester:Prateek Gupta
Editorialist:Hussain Kara Fallah

PROBLEM EXPLANATION

There are N hills located on a straight line. The height of the i^th one is denoted by H_i. A participant standing at the top of the i^th hill jumps to the nearest hill to the right which is strictly higher than the one he is standing on. If the nearest one is further than 100 hills away, he doesn't move anywhere.

Giving Q queries of 2 types:

The first type is given by (P,K) , a participant standing on the P^th hill is willing to perform K successive moves, what hill he will be ending at?

The second type is given by (L,R,X), for each hill between the L^th one and the R^th one (inclusive) should be increased by X (it may be negative).

DIFFICULTY:

medium

PREREQUISITES:

Complexity Analysis, Sqrt decomposition

EXPLANATION:

Let's define an array nxt[N] where nxt_i denotes the next hill the participant standing at the i^th hill is going to jump to (or nxt_i=i if he cannot jump to any other hill).

Let's break our hills into blocks, each block consisting of exactly $S=\sqrt{n}$ hills. As you can guess, keeping only the next hill we would jump to from each one, is not really effective. That's because jumping hills one by one will lead us to at least O(Q * K) solution which exceeds the time limit indeed. Maintaining a sparse table is not a really good idea also, because modifying an element in a sparse table may lead you modifying the whole table.

Let's make something similar to sparse table, Let's define a table F[N]. For the i^th hill let F_i denotes the furthest hill (which is located in the same bucket) that we can reach via successive jumps starting from the i^th hill (and how many jumps we need to reach it).

Assuming both of our tables F[],nxt[] are fixed, then answering queries of the first type would be quite easy. Let's repeatedly jump to the last hill in the current bucket as long as we are not exceeding the remaining jumps, after that moving 1 bucket forward via nxt[] table. So any number of jumps would be decomposed into at most $\sqrt{n}$ mass jumps. At a point if a bucket was longer to finish than the remaining jumps, let's just find our destination by processing it linearly. So the first query is answered in $O(\sqrt{n})$

Let's discuss modifying our arrays.

Regarding modifying heights, this is a naive application of sqrt decomposition which can be done in $O(\sqrt{n})$, by updating blocks which were included partially in the query in a linear search. Regarding blocks that were completely included into the query we may increment the variable denoting the sum of increments applied to this bucket (each bucket should have a variable).

Observations:

For each i such that (i > R) :: nxt_i will stay the same.

It's obvious because all participants are jumping to the right. Starting from the (R+1)^th hill, no hill will be changed.

For each i such that (i < L-100) :: nxt_i will stay the same, that's because a participant cannot skip more than 100 hills, so for each i in the previous range, (i+100 < L), so no participant would be allowed to jump to a hill that is modified through our query.

Consider the i^th hill, if nxt_i=j and we apply the QUERY(L,R,X) for any (L ≤ i AND R ≥ j) then the value of nxt_i won't change, that's because the j^th hill is the closest strictly higher hill (to the i^th one), and applying the same query to all hills between won't change the relative order between any pair of them.

For each i such that (R-100 < i ≤ R) :: nxt_i will be modified and needs to be calculated again.

For each i such that (L-100 ≤ i < L) :: nxt_i will be modified and needs to be calculated again.

As a conclusion, you can see that the nxt value of around 200 hills will be changed. We can process this in nearly O(400) by maintaining a stack. Regarding our table F modification, we should process each bucket that contains at least one hill which has its nxt variable modified. We should process each bucket linearly from right to left and maintain a stack during that. All modified buckets should have its data refreshed. Modification query can be done in $O(400 + \sqrt{n})$

AUTHOR'S AND TESTER'S SOLUTIONS:

AUTHOR's solution: Can be found here
TESTER's solution: Can be found here