can anyone help me in this problem , i am getting TLE in task 3 . I checked up the editorial and the approach seems almost similar. can anyone help?
here is the link to my submission.

Note - In the structure Node , mn is the minimum index of the string passing through it, and x is the index of the string ending at that leaf .
so mn is ids[0] and x is leaf_id if you co-relate solution with editor.

When and how will codechef contact college toppers who will be offered 100% scholarship for CCDSAP. And, also since I landed under top 20 Indians when will I get my laddus.

I know that I should keep patience but Since it is my first time, when I will get laddus, I am little excited about this.

Problem Link

Practice

Contest

Author:Rahim Mammadli

Tester:Misha Chorniy

Editorialist:Bhuvnesh Jain

Difficulty

EASY-MEDIUM

Prerequisites

Cross Product, Binary Search

Problem

Given a stationary point $P$ and a point $Q$ moving in straight line, indicate the time when $Q$ is visible from $P$, given that there am opaque sphere between them.

Explanation

We will try to find the solution in 2-D and then extend the idea to 3-D as well.

From the above figure, the first idea which can be clearly concluded is that, once point $Q$ becomes visible from $P$, it will remain visible forever. Before that, it will always remain invisible. This, the function (whether $Q$ is visible $P$ at given time $t$) follows the idea that it is false initially and after a certain point, it always remains true. This hints that we can binary search on the answer and just need to check whether the point $Q$ is visible from $P$ at given time $t$ or not. For more ideas on "Binary search" on such type of problem, refer to this awesome tutorial on topcoder. Hence, solution template looks like:

    double low = 0, high = 10^18
    for i in [1, 100]:
        double mid = (low + high) / 2
        if visible(P, Q, C, r, mid):
            high = mid
        else:
            low = mid
    double ans = (low + high) / 2

So, given a particular time $t$, we can first calculate the position of point $Q$. Join $P$ and $Q$ by a straight line. If the line doesn't pass through the circle, the point $Q$ is visible from $P$ else it is not visible. To check if a given line passes through the circle or not, it is enough to check that the perpendicular distance of the line from the centre, $C$, of the circle is greater than the radius, $r$, of the circle. For this, we first complete the triangle $PCQ$ and let the perpendicular distance of $PQ$ from $C$ be denoted by $CO$. Using the formula,

$$\text{Area of triangle} = \frac{1}{2} * \text{Base} * \text{Height} = \frac{1}{2} * CO * PQ$$

Since the area of the triangle can be found given 3 points in 2-D, and $PQ$ is the Euclidean distance between $P$ and $Q$, we can find the value of $CO$ efficiently. Finally, we just need to compare it to $r$, the radius of the circle.

For extending the solution in 3-D, the idea is same and we just need to find the area of a triangle in 3-D. For details, one can refer here. It can be clearly seen that the above formula holds for the 2-D case as well.

$$\text{Area of triangle in 2/3-D} = \frac{|CP X CQ|}{2}$$

where $CP$ and $CQ$ are vectors, $a X b$ denotes cross product of vectors and $|a|$ denotes the magnitude of vector.

Thus, to find the length of $CO$, we have

$$|CO| = \frac{2 * \text{Area of triangle PCQ}}{|PQ|} = \frac{|CP X CQ|}{|PQ|}$$

For more details, you may refer to the editorialist solution which exactly follows the above idea.

Extra Ideas/Caveats

The binary search implementation mentioned in the editorial is different from the one mentioned in Topcoder tutorial. Though both will give AC here, the one in Topcoder needs one to correctly set the Epsilon value for termination condition and sometimes can lead to wrong answers due to precision issues. The editorialist just prefers the above style to implement binary and ternary search involving doubles as calculation of epsilon is not required.

Note from the author

Finding the distance of a point from a line in 3-D is a generally common problem and also contains some edge cases where the point may not lie within the line segment region. But given the constraints of the problems, there are no edge cases but we should be aware of it in general.

Feel free to share your approach, if it was somewhat different.

Time Complexity

$O(1)$ per test case (around 100 iterations for binary search).

Space Complexity

$O(1)$

AUTHOR'S AND TESTER'S SOLUTIONS:

Author's solution can be found here.

Tester's solution can be found here.

Editorialist's solution can be found here.

First of all i would like to say, i am really sry but i am kind of worried about false positive MOSS hit i got in May18B. I totally understand codechef team is busy but it has been over 14 days since i submitted my request for restoration of rank through mail but i received no reply yet. (and i was kinda scared of ending up like this guy - https://discuss.codechef.com/questions/126366/damn-what-just-happened/126532)

According to the mail i received, the two solutions bellow were found same: https://www.codechef.com/viewsolution/18555493 (Mine) https://www.codechef.com/viewsolution/18408704 (Egors)

I would like to point out, that the solutions written by us are totally different and may have triggered the MOSS cuz of us using the same IO library (ya, i know we both didn't credit but i don't even remember where i got it from lol). A look at that those links can tell you that the time complexity of the solutions are different. (Mine is brute force and only passed 4 cases while egors passed all of them). Also, umm, the main code is totally different if you go into the main function.

At the end, i hope my ranking for May18B and solution will be restored.

Thanks

@admin@vijju123

I used the same approach as mentioned in the editorial using python 3. I am getting TLE for 6 out of 7 tasks.

The link for the code is:

Could anyone please check and see whats wrong with my code. I have been trying from many days but not able to understand why I am getting TLE. It will be of great help. Thanks!!

I am at that stage in programming that whenever I see a question related to trees or graphs I don't even read it and just skip it.I have no knowledge of trees or graphs but I want to learn them.I want help in how to start these topics and some problems(mostly basic) on them to gain some confidence. Can someone please help me or at least tell me the resources to start learning these topics.

Link to Problem:-https://www.codechef.com/problems/VEGETA My Solution:-https://www.codechef.com/viewsolution/18911997

Can anyone find what is mistake in my solution to the problem roads and libraries. I am getting a SIGSEGV error.

https://www.hackerrank.com/challenges/torque-and-development/forum/comments/454647

I am trying this problem on longest palindromic subsequence. https://www.spoj.com/problems/JEWELS/ Here is my code- https://pastebin.com/sDKrqg5g I am unable to find the bug.Kindly help.Kindly tell how to approach this problem,how to calculate the center of the longest palindromic subsequence

Problem Link

Practice

Contest

Author:Noszály Áron

Tester:Misha Chorniy

Editorialist:Bhuvnesh Jain

Difficulty

EASY

Prerequisites

BFS/Floyd Warshall, Observations

Problem

You are to convert number $A$ to number $B$ using the following operation in the minimum number of steps:

• Write A as a binary number with arbitrary number of leading zeros (possibly none)
• Shuffle the binary digits of the A in an arbitrary order. Call it $A'$
• The output is $(A' + 1)$. Let us call this number as $X$.

Remember the notation of $A'$ and $X$ as it is used everywhere in the editorial.

Explanation

Subtask 1: A, B ≤ 128

The problem asks to minimise the number of steps to go from $A$ to $B$. Generally, these type of problems can be easily modelled as a graph and perform BFS to find the answer. Here is a general idea:

Let us model each step as an edge from initial number to final number with an edge of some cost. So, the path with the smallest weight from source to destination is the required answer and also gives us a way to achieve the transition.

In this problem, we can just do what the operations ask us to do. Just all possible shuffling of the digits of A in binary representation and consider only those ones which give end result within the desired range ([0, 128]). Let us call this number as $X$. Add an edge of weight $1$ from $A$ to $X$. Build the complete graph based on all possible transitions. Make sure that this graph will be directed one as transforming from $A$ to $X$ might not be the same as transforming from $X$ to $A$ due to the last operation which adds $1$ to the result. Once, we have the directed graph, we can simply perform any all pair shortest path algorithm like BFS, Floyd Warshall (or Dynamic Programming as a graph is directed) and precalculate the answer for all possible cases. Once, the answers are precalculated, each test case can be answered in constant complexity. For more details, one can refer to the editorialist solution below.

The maximum number of edges from a number $A$ emerging out will be $7! = 5040$ in the worst case, but in practice, it will be quite less. The number of vertices in the graph will be $128$. Using Floyd Warshall algorithm the precomputation can be achieved in $O(128^3)$, i.e. $O(A^3)$. This is enough to solve this subtask.

Subtask 2: A, B ≤ ${10}^{18}$

The constraints in this subtask are quite large and the number of test cases also suggest we need a logarithmic approach. This leads us to write $A$ and $B$ in binary representation and finding some observations to proceed with the solution.

Let us first simplify the approach by trying to convert $A$ to $(B-1)$ as in the end $1$ would be added as part of the last operation.

We can see that in one step we can shuffle the digits of $A$ in such a manner that an extra $1$ is introduced in the binary representation of the newly formed number. This can be done by simply shuffling the digits to contain binary digit $1$ from the ${2}^{nd}$ position. For example: Let $A = 3$. In binary representation $A = 011$. We can shuffle the digits as $A' = 110$. On adding $1$, we get $X = 111$, i.e. $X = 7$. Thus, we can introduce a binary digit $1$ in one step.

Also, we can decrease any number of binary digit $1$ from $A$. This can be done by easily placing the required in the number of $1$ in towards the end, followed by a $0$ and then placing the digits in any order we like. For example: Let $A = 13$, i.e. $A = 1101$ in binary representation. Say we want to decrease one binary digit $1$, we can arrange the digits as $A' = 1011$. On adding $1$, we get $X = 1100$. If we wanted to decrease two binary digit $1$, we can arrange the digits as $A' = 0111$. On adding $1$, we get $X = 1000$. Thus, we decrease any number of binary digit $1$ in one step.

With the above 2 scenarios, the following is the algorithm-

1. Find the number of ones in the binary representation of $A$ and $(B - 1)$. Let us denote then by $OA$ and $OB$
2. If $OA > OB$, then we can achieve the operation in $2$ steps. First decreasing the number of ones in the first step and then rearranging the digits in another step.
3. If $OA <= OB$, then we need $(OB - OA)$ steps to first make the number of ones equal (see decrease operation takes place at one step each). Finally, we can arrange the digits to achieve the desired number.

The only corner case is as follows:

1. If $B$ is $0$ then, we can't achieve the desired state whatever the value of $A$ is. Since we are adding $1$ in the last step we are guaranteed to have atleast one binary digit $1$ in binary representation. Thus the answer for this case is $-1$.
2. If $B$ is $1$ then, we can achieve the desired state only if $A = 0$, in one step. In another case, it is impossible as even though decreasing the number of binary digit $1$, the end result would be a number greater than $1$. So the answer is $1$ if $A = 0$, else $-1$.

The number of ones in binary representation can be calculated using the below pseudo-code:

    def count_ones(integer x):
        ones = 0
        while x > 0:
            if x % 2 == 1:
                ones += 1
            x /= 2
        return ones

Feel free to share your approach, if it was somewhat different.

Time Complexity

$O(\log{A} + \log{B})$ per test case.

Space Complexity

$O(1)$

AUTHOR'S AND TESTER'S SOLUTIONS:

Author's solution can be found here. (It will pass subtask 1 only and uses dynammic programming approach)

Tester's solution can be found here.

Editorialist's solution for subtask 1 can be found here.

Editorialist's solution for full problem can be found here.

T= int(input()) for i in range(T): n= int(input())

s=input().split()
count = 0
what = 0
for i in s:
    if i == s[0] :
        count=count+1
    elif i == s[1]:
        what = what+1

if count==what :
    print('Draw')
elif count>what :
    print(s[0])
else :
    print(s[1])

Can anyone please look why Im getting wrong answer.

problem link:-link text

My solution:link text

When I ran three loops for few n (size), I noticed that all combinations are not to be checked . Hence I reduced almost 2 loops but im getting wrong answer.

Thanks

Can anyone help me with the solution of this problem? https://www.codechef.com/QUCO2018/problems/BEERUS/

Thanks in advance :)

PROBLEM LINK:

Contest
Practice

Author:Amit Kumar Pandey
Editorialist:Amit Kumar Pandey

DIFFICULTY:

SIMPLE

PREREQUISITES

Maths

PROBLEM:

Ironman wants to build his new core. For that, he inputs three random number x, y and z in Jarvis. Help Jarvis determine whether those three numbers are taken as sides form the isosceles triangle or not.

EXPLANATION:

A triangle is a 3-sided polygon.
We are given the length of three sides.
The condition for forming the triangle is the the sum of the two side of triangle must be greater than third side. If this condition satisfies then we have to find whether triangle is equilateral, isosceles or scalene triangle. 1. If all sides of the triangle are equal then it is equilateral.
2. If two sides are equals then the triangle is isosceles. If we find any isosceles triangle then we have to add one to counter variable because we have to print the total number of the isosceles triangle in the output.
3. else the triangle is scalene.

If the property of triangle doesn't get satisfied then we have to print "not triangle".

AUTHOR'S AND EDITORIALIST'S SOLUTIONS:

Author's solution can be found here.
Editorialist's solution can be found here.

RELATED PROBLEMS:

AVHNTRI

PROBLEM LINK:

Contest
Practice

Author: Mrinal Sinha
Editorialist: Mrinal Sinha
Tester:Amit Kumar Pandey

DIFFICULTY:

EASY

PREREQUISITES:

Math

PROBLEM:

Starlord is stuck in space on his way back after a successful mission when his spacecraft crashed. He now has to go jumping from asteroid to asteroid to get to a nearby space camp. The asteroids are in such an order that their lengths increase to a certain extent as he jumps to the next asteroid. The series of the lengths of the asteroids is given below. For a given asteroid, you have to determine whether it comes in his path or not. Series: 44, 120, 304, 736

EXPLANATION:

The series given here is an Arithmetico-Geometrico Series with numbers written as 11 * 4, 15*8, 19*16 and 23*32 respectively. Thus the first term of the A.P is 11 with common difference 4 whereas the first term of G.P is 4 with common ratio 2. With the help of above values we can determine the previous positive values which will be 7*2 =14 and 3*1 = 3.
Thus the general formula for the above expression is (a+(n-1)*d)*(b*pow(r,n-1)), where ‘a’ is the 1^st term of the A.P (which is 3), ‘d’ is the common difference of the A.P (which is 4), ‘b’ is the 1^st term of G.P (which is 1), ‘r’ is the common ratio of the G.P (which is 2) and ‘n’ is the n^th term of the series.
Thus initialize n with 1 and calculate the value of above expression.

Thus initialize n with 1 and calculate the value of above expression.
If the value is equal to the given number, then print “YES”.
If the value is greater than the given number ,then print “NO”.
*If the value is less than the given number, then increment n by 1 and again check whether the value of the expression is greater than or equal to the given number. Do this step until the 1^st or 2^nd step is satisfied.

AUTHOR'S AND EDITORIALIST'S SOLUTIONS:

Author's solution can be found here.
Editorialist's solution can be found here.
Tester's solution can be found here.

Hello everyone,

I like Programming very much but due to some reasons, I am not able to perform well. Most of the time I get "wrong answer" even if it seems to be correct(may be due to it isn't working for even 1 test case). So please tell me some tricks and tips which would help me. Such as how to test your program, must know algorithms, the way you follow while coding or anything else.

Thank You in advance.

Problem Link

Practice

Contest

Author:Jitender

Tester:Misha Chorniy

Editorialist:Bhuvnesh Jain

Difficulty

EASY-MEDIUM

Prerequisites

Tries, Offline querying

Problem

You a given $N$ strings and $Q$ queries. For each query, given $R$ and string $P$, you need to find the lexicographically smallest string which has the largest common prefix with $S$.

Explanation

Subtask 1: N, Q ≤ 1000

A simple brute force which checks each string from index $1$ to $R$ and stores the answer at each step will suffice. Below is a pseudo-code for it:

    def find_max_prefix_match(string a, string b):
        ans = 0
        for i in [0, len(a), len(b) - 1]:
            if a[i] == b[i]:
                ans += 1
            else:
                break
        return ans

    def solve_query(index R, string P):
        ans = ""
        prefix = 0
        for i in [1, n]:
            if find_max_prefix_match(S[i], P) > prefix:
                prefix = find_max_prefix_match(S[i], P)
                ans = S[i]
            else if find_max_prefix_match(S[i], P) == prefix:
                ans = min(ans, S[i])
        return ans

The complexity of the above approach is $O(N * Q * 10)$ in the worst case as the maximum size of the string can be at most 10.

Subtask 2: N, Q ≤ 100000

The first idea which comes whenever you see string problems deal with prefixes if using tries or hashing. In this problem too, we will use trie for solving the problem. In case you don't know about it, you can read it here.

Let us first try to understand how to find the lexicographically smallest string with largest common prefix with $P$. Assume we have the trie of all the strings build with us. We just start traversing the Trie from the root, one level at a time. Say we are at level $i$, we will try to greedily go to the node whose character matches with our current character, $P[i]$. This will help us to maximise the longest common prefix. The moment we find a mismatch, i.e. a node with current character doesn't exist, we will try to now greedily find the lexicographically find the smallest string. For this, we just keep on traversing down the left-most node in the trie till a complete work is found.

But the above approach works when $R = N$ in all queries as without it we can't identify whether the string we are traversing lies in the required range of the query or not.

There are 2 different approaches to the full solution, Online solution and Offline solution.

Author/Tester Solution: Offline Approach

The problems where we can easily solve a problem given a full array but need to query for a prefix of the array can be easily handled using offline queries. The idea is as follows:

We first sort the queries based on the index of the array given. We now build out data structure (here trie), incrementally. Say the data structure is built using all the first $i$ elements, we now answer every query which has an index as $i$ in the query.

The pseudo-code for it is below:

    queries = []
    for i in [1, q]:
        r, p = input()
        queries.push((r, p, i))
    queries.sort()

    cur_index = 0
    for (r, p, i) in queries:
        while (cur_index <= r):
            insert_element_to_ds_trie
            cur_index += 1
        ans[i] = query_from_ds_trie(S)      //parameter r is not required

    for i in [1, q]:
        print ans[i]

For more details, you can refer to the author's or tester's solution below.

Editorialist Solution: Online Solution

The idea is simple. With every node in the trie, we keep a vector of indices which it is a part of. Using this vector we can easily decide whether the string we are traversing lies within our required range or not. But before discussing the full solution, we need to be sure that this will fit into memory limits because seeing it in a naive manner seems to consume quadratic memory as each node can have a vector of length $N$.

To prove that the above-modified trie also uses linear memory in order of sum of the length of strings, we see that each index appears in any vector of a node in trie as many characters are there in the string. So, out trie just uses twice the memory that the normal trie (the one in author or tester solution) uses.

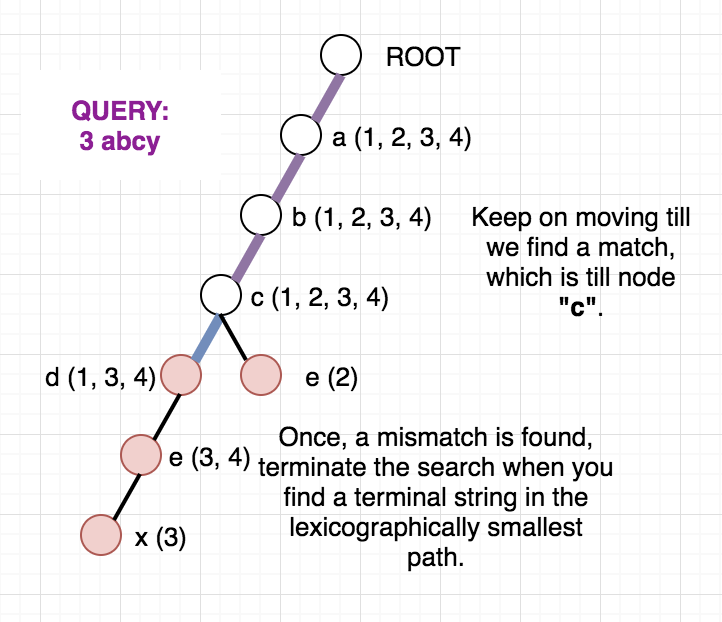
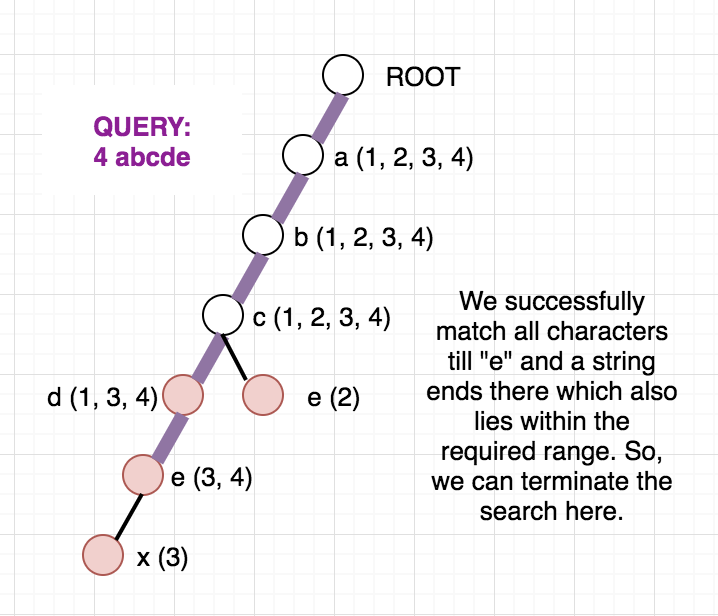
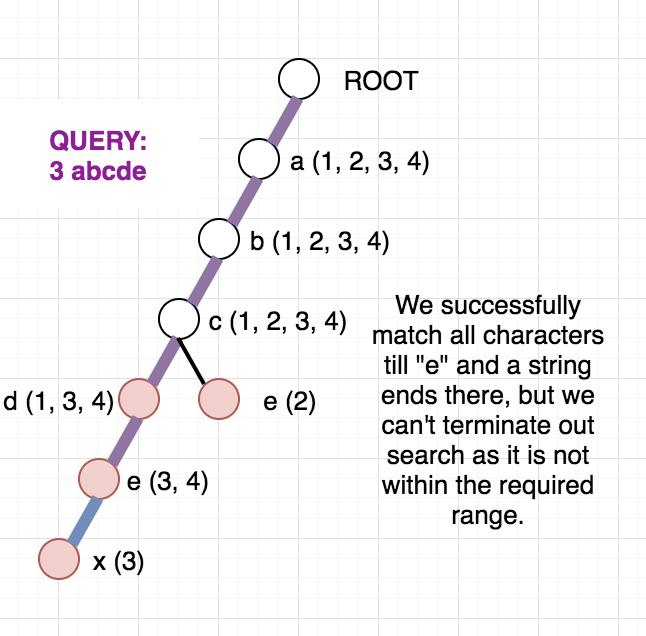
Once, the above modified Trie is built, we can answer our queries easily. Since the strings are added incrementally, we are sure that the vector containing the indices will always be in sorted order. To check whether any string at a given node lies in modified range, we can use binary search. But, we can be clever here too, as the binary search will be an overkill. Since the range we want is always a prefix of the array we can just check the first element of the vector and decide whether any string lies in the required range or not. To get a clear picture of the above, you can see the below picture of the trie build from the sample case in the problem. It also contains how the answer to different queries are arrived at.

Once, you are clear with the above idea, you can see the editorialist implementation below for help.

Feel free to share your approach, if it was somewhat different.

Time Complexity

$O(Q\log{Q} + \text{Sum of length of strings} * \text{ALPHABET})$ for offline solution

$O(\text{Sum of length of strings} * \text{ALPHABET})$ for online solution

where $\text{ALPHABET} = $ number of distinct english character (26 for this problem).

Space Complexity

$O(\text{Sum of length of strings})$

AUTHOR'S AND TESTER'S SOLUTIONS:

Author's solution can be found here.

Editorialist's solution can be found here.

Hey,all
Can someone help me in finding the error in logic as my last case is not passing. Any help would be appreciated.
My logic
I have taken two set one set will contain all the ingredients found on islands is it size comes out not equal to k then we will print sad.
If it's size becomes equal to k then we will check the size of other set is n if it is n it means we have taken ingredients from every islands so the size becomes n which is equal to no of islands so we will print all.
else we will print sad.

PROBLEM
My Solution

Tips for Optimizing C/C++ Code

1.Code for correctness first, then optimize!

• This does not mean write a fully functional ray tracer for 8 weeks, then optimize for 8 weeks!

• Perform optimizations on your ray tracer in multiple steps.

• Write for correctness, then if you know the function will be called frequently, perform obvious optimizations.

• Then profile to find bottlenecks, and remove the bottlenecks (by optimization or by improving the algorithm). Often improving the algorithm drastically changes the bottleneck – perhaps to a function you might not expect. This is a good reason to perform obvious optimizations on all functions you know will be frequently used.

2.People I know who write very efficient code say they spend at least twice as long optimizing code as they spend writing code.

3.Jumps/branches are expensive. Minimize their use whenever possible.

• Function calls require two jumps, in addition to stack memory manipulation.

• Prefer iteration over recursion.

• Use inline functions for short functions to eliminate function overhead.

• Move loops inside function calls (e.g., change for(i=0;i<100;i++) DoSomething(); into DoSomething() { for(i=0;i<100;i++) { ... } } ).

• Long if...else if...else if...else if... chains require lots of jumps for cases near the end of the chain (in addition to testing each condition). If possible, convert to a switch statement, which the compiler sometimes optimizes into a table lookup with a single jump. If a switch statement is not possible, put the most common clauses at the beginning of the if chain.

4.Avoid/reduce the number of local variables.

• Local variables are normally stored on the stack. However if there are few enough, they can instead be stored in registers. In this case, the function not only gets the benefit of the faster memory access of data stored in registers, but the function avoids the overhead of setting up a stack frame.

• (Do not, however, switch wholesale to global variables!)

5.Reduce the number of function parameters.

• For the same reason as reducing local variables – they are also stored on the stack.

6.If you do not need a return value from a function, do not define one.

7.Try to avoid casting where possible.

• Integer and floating point instructions often operate on different registers, so a cast requires a copy.

• Shorter integer types (char and short) still require the use of a full-sized register, and they need to be padded to 32/64-bits and then converted back to the smaller size before storing back in memory. (However, this cost must be weighed against the additional memory cost of a larger data type.)

8.Use shift operations >> and << instead of integer multiplication and division, where possible.

9.Simplify your equations on paper!

• In many equations, terms cancel out... either always or in some special cases.

• The compiler cannot find these simplifications, but you can. Eliminating a few expensive operations inside an inner loop can speed your program more than days working on other parts.

10.Consider ways of rephrasing your math to eliminate expensive operations.

• If you perform a loop, make sure computations that do not change between iterations are pulled out of the loop.

• Consider if you can compute values in a loop incrementally (instead of computing from scratch each iteration).

11.Avoid unnecessary data initialization.

• If you must initialize a large chunk of memory, consider using memset().

1216. For most classes, use the operators += , -= , *= , and /= , instead of the operators + , - , * , and / .

• The simple operations need to create an unnamed, temporary intermediate object.

• For instance: Vector v = Vector(1,0,0) + Vector(0,1,0) + Vector(0,0,1); creates five unnamed, temporary Vectors: Vector(1,0,0), Vector(0,1,0), Vector(0,0,1), Vector(1,0,0) + Vector(0,1,0), and Vector(1,0,0) + Vector(0,1,0) + Vector(0,0,1).

• The slightly more verbose code: Vector v(1,0,0); v+= Vector(0,1,0); v+= Vector(0,0,1); only creates two temporary Vectors: Vector(0,1,0) and Vector(0,0,1). This saves 6 functions calls (3 constructors and 3 destructors).

13.For basic data types, use the operators + , - , * , and / instead of the operators += , -= , *= , and /= .

14.Delay declaring local variables.

• Declaring object variable always involves a function call (to the constructor).

• If a variable is only needed sometimes (e.g., inside an if statement) only declare when necessary, so the constructor is only called if the variable will be used.

15Avoid dynamic memory allocation during computation.

• Dynamic memory is great for storing the scene and other data that does not change during computation.

• However, on many (most) systems dynamic memory allocation requires the use of locks to control a access to the allocator. For multi-threaded applications that use dynamic memory, you may actually get a slowdown by adding additional processors, due to the wait to allocate and free memory!

• Even for single threaded applications, allocating memory on the heap is more expensive than adding it on the stack. The operating system needs to perform some computation to find a memory block of the requisite size.

Can anyone help me out:

https://www.codechef.com/viewsolution/18917156