Problem Link

Practice

Contest

Author:Jitender

Tester:Misha Chorniy

Editorialist:Bhuvnesh Jain

Difficulty

EASY-MEDIUM

Prerequisites

Tries, Offline querying

Problem

You a given $N$ strings and $Q$ queries. For each query, given $R$ and string $P$, you need to find the lexicographically smallest string which has the largest common prefix with $S$.

Explanation

Subtask 1: N, Q ≤ 1000

A simple brute force which checks each string from index $1$ to $R$ and stores the answer at each step will suffice. Below is a pseudo-code for it:

    def find_max_prefix_match(string a, string b):
        ans = 0
        for i in [0, len(a), len(b) - 1]:
            if a[i] == b[i]:
                ans += 1
            else:
                break
        return ans

    def solve_query(index R, string P):
        ans = ""
        prefix = 0
        for i in [1, n]:
            if find_max_prefix_match(S[i], P) > prefix:
                prefix = find_max_prefix_match(S[i], P)
                ans = S[i]
            else if find_max_prefix_match(S[i], P) == prefix:
                ans = min(ans, S[i])
        return ans

The complexity of the above approach is $O(N * Q * 10)$ in the worst case as the maximum size of the string can be at most 10.

Subtask 2: N, Q ≤ 100000

The first idea which comes whenever you see string problems deal with prefixes if using tries or hashing. In this problem too, we will use trie for solving the problem. In case you don't know about it, you can read it here.

Let us first try to understand how to find the lexicographically smallest string with largest common prefix with $P$. Assume we have the trie of all the strings build with us. We just start traversing the Trie from the root, one level at a time. Say we are at level $i$, we will try to greedily go to the node whose character matches with our current character, $P[i]$. This will help us to maximise the longest common prefix. The moment we find a mismatch, i.e. a node with current character doesn't exist, we will try to now greedily find the lexicographically find the smallest string. For this, we just keep on traversing down the left-most node in the trie till a complete work is found.

But the above approach works when $R = N$ in all queries as without it we can't identify whether the string we are traversing lies in the required range of the query or not.

There are 2 different approaches to the full solution, Online solution and Offline solution.

Author/Tester Solution: Offline Approach

The problems where we can easily solve a problem given a full array but need to query for a prefix of the array can be easily handled using offline queries. The idea is as follows:

We first sort the queries based on the index of the array given. We now build out data structure (here trie), incrementally. Say the data structure is built using all the first $i$ elements, we now answer every query which has an index as $i$ in the query.

The pseudo-code for it is below:

    queries = []
    for i in [1, q]:
        r, p = input()
        queries.push((r, p, i))
    queries.sort()

    cur_index = 0
    for (r, p, i) in queries:
        while (cur_index <= r):
            insert_element_to_ds_trie
            cur_index += 1
        ans[i] = query_from_ds_trie(S)      //parameter r is not required

    for i in [1, q]:
        print ans[i]

For more details, you can refer to the author's or tester's solution below.

Editorialist Solution: Online Solution

The idea is simple. With every node in the trie, we keep a vector of indices which it is a part of. Using this vector we can easily decide whether the string we are traversing lies within our required range or not. But before discussing the full solution, we need to be sure that this will fit into memory limits because seeing it in a naive manner seems to consume quadratic memory as each node can have a vector of length $N$.

To prove that the above-modified trie also uses linear memory in order of sum of the length of strings, we see that each index appears in any vector of a node in trie as many characters are there in the string. So, out trie just uses twice the memory that the normal trie (the one in author or tester solution) uses.

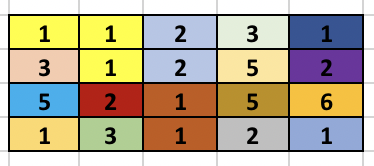
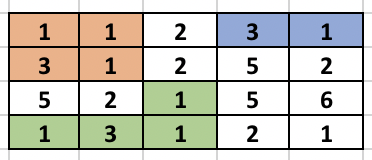
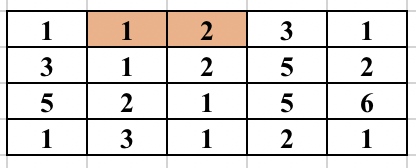
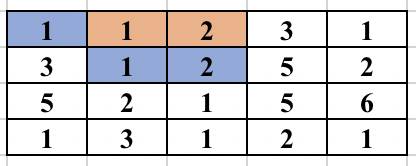
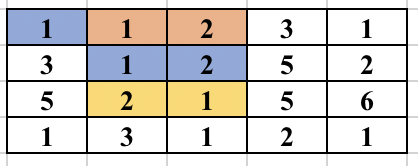
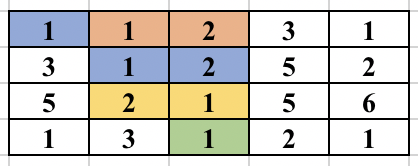
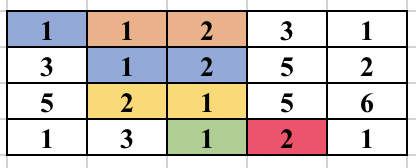
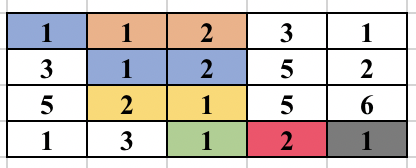
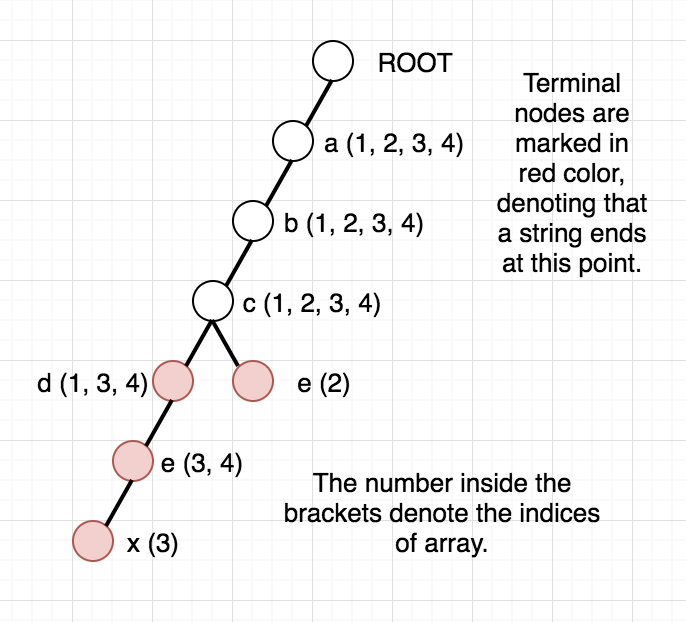
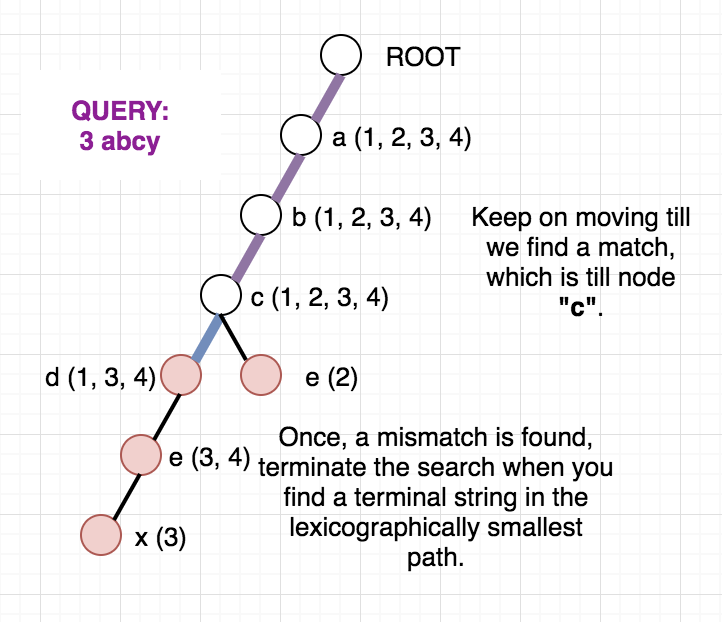
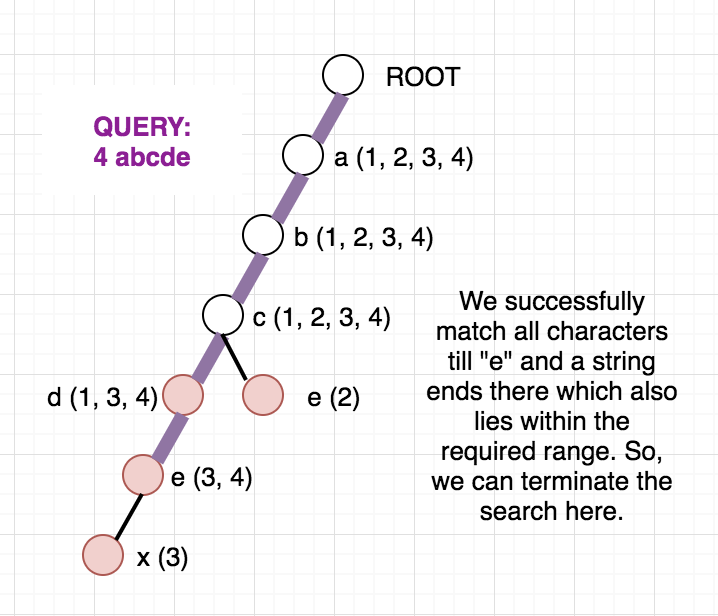
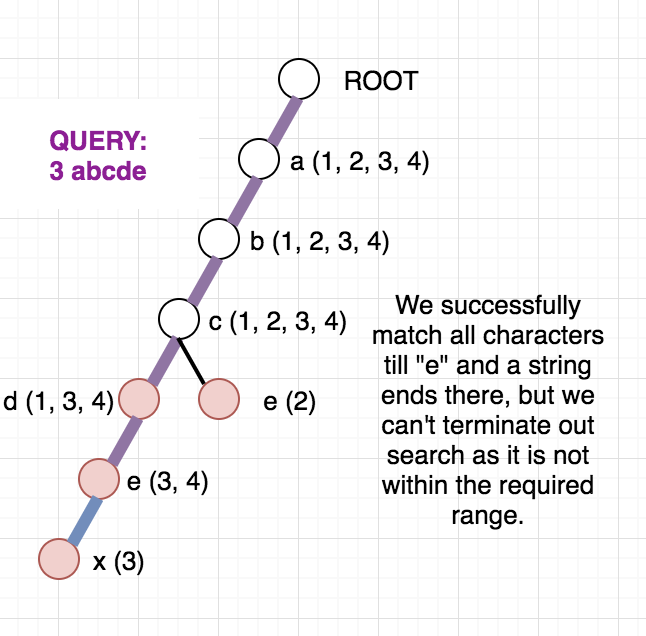
Once, the above modified Trie is built, we can answer our queries easily. Since the strings are added incrementally, we are sure that the vector containing the indices will always be in sorted order. To check whether any string at a given node lies in modified range, we can use binary search. But, we can be clever here too, as the binary search will be an overkill. Since the range we want is always a prefix of the array we can just check the first element of the vector and decide whether any string lies in the required range or not. To get a clear picture of the above, you can see the below picture of the trie build from the sample case in the problem. It also contains how the answer to different queries are arrived at.

Once, you are clear with the above idea, you can see the editorialist implementation below for help.

Feel free to share your approach, if it was somewhat different.

Time Complexity

$O(Q\log{Q} + \text{Sum of length of strings} * \text{ALPHABET})$ for offline solution

$O(\text{Sum of length of strings} * \text{ALPHABET})$ for online solution

where $\text{ALPHABET} = $ number of distinct english character (26 for this problem).

Space Complexity

$O(\text{Sum of length of strings})$

AUTHOR'S AND TESTER'S SOLUTIONS:

Author's solution can be found here.

Editorialist's solution can be found here.

Someone, please explain what is the meaning of parity of permutation and how it can be helpful.

And also how can we implement it?

Can you post some question related to it practice...

Thank you.

how to create a vector of maps and how to store values in it and how to print those values??

Hey guys, Can anybody explain why am i getting tle on the below mentioned problem. I checked it with the accepted solutions but can't find any difference. Problem: https://www.spoj.com/problems/ABCPATH/ My solution: https://ideone.com/BCAd0l

import java.util.*;
import java.lang.*;

class VOTERS{
    public static void main(String[] args){
    Scanner scanner = new Scanner(System.in);
    int N1 = scanner.nextInt();  // number of voters in first list
    int N2 = scanner.nextInt();  //  "     "   "     "  second "
    int N3 = scanner.nextInt();  //  "     "   "     "  third "

    int[] firstList = new int[N1];
    int[] secondList = new int[N2];
    int[] thirdList = new int[N3];
    for(int i=0;i<N1;i++){
        firstList[i] = scanner.nextInt();
    }
    for(int i=0;i<N2;i++){
        secondList[i] = scanner.nextInt();
    }
    for(int i=0;i<N3;i++){
        thirdList[i] = scanner.nextInt();
    }
    HashMap<Integer, Integer> countMap = new HashMap<Integer, Integer>();
    for(int i=0;i<N1;i++){
        if(countMap.containsKey(firstList[i])){
        countMap.put(firstList[i], countMap.get(firstList[i]) + 1);
        }
        else{
        countMap.put(firstList[i], 1);
        }
    }
    for(int i=0;i<N2;i++){
        if(countMap.containsKey(secondList[i])){
        countMap.put(secondList[i], countMap.get(secondList[i]) + 1);
        }
        else{
        countMap.put(secondList[i], 1);
        }
    }
    for(int i=0;i<N3;i++){
        if(countMap.containsKey(thirdList[i])){
        countMap.put(thirdList[i], countMap.get(thirdList[i]) + 1);
        }
        else{
        countMap.put(thirdList[i], 1);
        }
    }
    ArrayList<Integer> result = new ArrayList<Integer>();
    for(Map.Entry<Integer, Integer> entry : countMap.entrySet()){
        if(entry.getValue() > 1){
        result.add(entry.getKey());
        }
    }
    System.out.println(result.size());
    for(int i=0;i<result.size();i++){
        System.out.println(result.get(i));
    }
    }
}

f(n) = int(n)+1(if fractional part of n is >= 0.5) else f(n) = int(n).

In an array a of n elements . sum = 0; for(i=0; i<n; i++) { for(j=0; j<n; j++) { sum += f(a[i] / a[j]); } } 1<= n <=10^5 1<= a[i] <=10^5 Ex - for array 1 2 3 4 the value of sum is 22.

If a=3 and n=input().split() And there are "a" no. Of values ,means 3 values and how will we convert it into integers

Problem Link

Practice

Contest

Author:Stacy Hong

Tester:Misha Chorniy

Editorialist:Bhuvnesh Jain

Difficulty

MEDIUM

Prerequisites

BFS, DFS, DSU, Sorting

Problem

You are given a grid with numbers written on every cell. You are required to find the largest connected component on the grid such that it contains at most 2 distinct numbers in it.

Note that editorial refers to the flowers as numbers.

Explanation

Subtask 1: N, M ≤ 100

A simple brute force which considers every pair of different numbers and performs BFS on the grid to find the connected component and their sizes is enough to pass this subtask. Below is a pseudo-code for it.

    def solve(c1, c2):
        res = 0
        for i in [1, n]:
            for j in [1, m]:
                if vis[i][j] or (a[i][j] != c1 and a[i][j] != c2):
                    continue
                # perform bfs to find size of connected component containing c1 and c2
                # update res variable with maximum value
        return res

    ans = 0
    for c1 in [1, 100]:
        for c2 in [i, 100]:
            # also handle case of one color only.
            ans = max(ans, solve(c1, c2))

The time complexity of the above approach is $O(n * m * {\text{Max(a[i][j])}}^{2})$.

Subtask 2, 3: N, Q ≤ 2000

The solution approach for last 2 subtasks is same. Just difference in implementation and constant factors can lead to passing subtask 2 only.

The full solution idea relies on the brute force solution above. Instead of doing a complete BFS on the grid every time based on the type of colour you need to consider, we store the edges containing different numbers and do BFS/DSU on it. Below are the 2 different approaches for it.

Author/Tester Solution: DSU + Sorting/HashMap

First find all connected components which have the same type of numbers. Store with each component the size of the component and the index of the component as well. This can be easily done with a BFS/DFS. Now create edges between 2 component which are adjacent to each other in the grid i.e. there exists a cell in component $1$ which is adjacent to a cell in component $2$. Store the edges in the following format:

$$\text{{Number in component 1, Number in component 2, Index of component 1, Index of component 2}}$$

To avoid doing the same computation again, store only the edges such that $\text{Number in component 1} < \text{Number in component 2}$. This will help to reduce the constant factor by 2 in your code.

Now, we traverse each edge based on the numbers they connect and perform DSU to find the maximum connected component. Below is the explanation of sample test case in the problem.

The left side image shows the different components formed after the first BFS is done. The second side image shows the result of performing DSU. So, once the BFS is done, we see that cell $(2, 1)$ containing $3$ is adjacent to cell $(1, 1)$ containing $1$, so we merge them using DSU. Again cell $(4, 1)$ containing $1$ is adjacent to cell $(4, 2)$ containing $3$ so, we merge them using DSU. The process continues as cell $(4, 3)$ containing $1$ is adjacent to $(4, 2)$ containing $3$ (which was already expanded before) and the component increases.

The only issue which needs to be taken care while implementing the above solution is resetting of DSU after every iteration. Doing it in naive manner i.e. resetting all the components to original sizes and parent as themselves will TLE even for subtask 2 as the complexity will be similar to subtask 1. Instead, we only restore the values whose parent or size changed while performing the DSU operation. This can be stored while performing the merge operation.

For more details, you can refer to the author's or tester's solution below.

The complexity of the above approach will be $O(n * m * log(n * m))$ as you will traverse each edge once. The logarithmic factor is due to sorting or using maps to store the edges. If you use hash-maps instead to store the edges, the complexity will be $O(n * m)$ but will large constant factor.

Editorialist Solution: Edge-based Graph traversal

UPDATE: This solution is slow. The author created a counter test against it. The time complexity will be $O(n^2*m^2)$ as pointed out in comments below. Even the test case provided is similar. Please refer to author's solution above for full problem. Will ask Codechef team to add that case in the practice section too for help.

Instead of forming any components or performing DSU or doing BFS like the normal way, we see simple observation in the brute force approach. If, each edge connecting adjacent cells in the grid, whether having same numbers or different numbers if traversed at most twice while determining the size, the complexity will be $O(8 * n * m)$ overall. Below is the detailed description of the idea:

First, select an edge in the grid. Find the numbers (at most 2) which will form the component. We will try to find the full component which contains this edge and make sure this component is traversed only once. For this, you start a normal BFS from each cell. You go to adjacent cell only if it is one of the 2 required numbers. While adding the node in the BFS queue, we all update the possible ways in which the edge could be traversed as part of the same component. So, cell $(3, 2)$ containing $2$ was visited from cell $(2, 2)$ containing $1$. But it could be traversed from cell $(3, 3)$ containing $1$ in future and will form the same component. So, we update all 4 directions of a cell can be visited in the same component before adding the cell in BFS queue. The BFS for a component is performed only if the edge was never traversed before in any component. The image below shows how the component is expanded in each step of BFS when the starting edge is selected as $(1, 2)$ and $(1, 3)$.

The time complexity of the above approach is $O(n^2*m^2)$ and will pass subtask 1 only.

Once, you are clear with the above idea, you can see the editorialist implementation below for help.

Feel free to share your approach, if it was somewhat different.

Time Complexity

$O(n * m)$

Space Complexity

$O(n * m)$

AUTHOR'S AND TESTER'S SOLUTIONS:

Author's solution can be found here.

Tester's solution can be found here.

Editorialist's solution can be found here. (Will TLE).

Problem Link

Practice

Contest

Author:Stacy Hong

Tester:Misha Chorniy

Editorialist:Bhuvnesh Jain

Difficulty

HARD

Prerequisites

Branch and Bound, Dynamic Programming, Big Integers, Hashing, DFS/Recursion

Problem

You are given a string $S$ and integer $N$. So need to place some '+' symbols in the strings $S$ so that the value of the expression equals $N$.

Explanation

Subtask 1: N < 1000000

A simple knapsack like dynamic programming is sufficient to pass this subtask. The dp state is as follows:

$$dp[i][j] = \text{1 if first 'i' characters of S can be partitioned such that the sum is 'j' else 0}$$

A recursive pseudo-code for the above logic is given below:

    def solve(int idx, int remain):
        if idx == len(s):
            return remain == 0
        if dp[idx][remain] != -1:
            return dp[idx][remain]
        dp[idx][remain] = 0
        num = 0
        for i in [idx, len(s) - 1]:
            num = num * 10 + s[i] - '0'
            if (num > remain):
                break
            if (solve(i + 1, remain - num)):
                PLUS[i] = 1;
                return dp[idx][remain] = 1
        return dp[idx][remain];

    solve(0, N)     # N = integer value of string s in input
    for i in [0, len(s) - 1]:
        if i and PLUS[i]:
            print '+'
        print s[i]

The above code works in time complexity $O(|S| * N)$ where $|S|$ is the length of string $S$ and $N$ is the given integer. The space complexity is also same. Note that Codechef servers allow programs using such large memory (around 1G) to pass but you can you bitset or other equivalent structures to reduce the memory of your program too. See the linked solution below for subtask 1 for more details.

The solution for this subtask also exists using hashing and dynamic programming.

Subtask 2: N < |S|

Adding 2 numbers of sizes $x$ and $y$ leads to final result having size at most $max(x, y) + 1$. This is easy to prove. The size will be $max(x, y)$ if there is no carry-over in the end otherwise it will increase by 1. Extending the above logic to addition of $m$ number, we can conclude that if the numbers have lengths $x_1, x_2, \cdots, x_m$, then the length of final result is bounded by $(max(x_1 + x_2 + \cdots + x_m) + m - 1)$. You can easily prove it using induction.

Note that number of ways to partition the string $S$ into different expression is exponential. But using the above observation, you can the conclude the following fact:

Given a string $S$ and integer $N$, having the length as $n$, there is very less number way to achieve the target $N$ if $n$ is comparable to $|S|$. This is because most of the partitions will either have the maximum number in them as too low. Equivalently, if the number of partitions we put in $S$ is large, then achieving a larger target $N$ is not possible. This hints that for sufficiently large integers, the greedy technique of choosing a larger size partition and checking if the remaining part can add up to desired $N$ will run very fast in practice as the number of iterations will not be large. For example: $S = 114390211, N = 43915$

Considering greedily large size partition of $S$ such that their value is less than $N$, we have the following numbers: [11439, 14390, 43902, 39021]. (Note that the size of this selected numbers can be at most (|S| - n + 1).) Let us greedily start with $43902$. The remaining parts of $S$ are $(11, 11)$ and the required sum now is $(43915 - 43902) = 13$. Note that there are 2 ways to achieve it $(11 + 1 + 1) \text{ or } (1 + 1 + 11)$. As you can see, the number of iterations were less. The example is just a short one to make to understand how greedy recursion might behave for larger test cases.

But the other case where the integer $N$ is small but $|S|$ is very large, there can be large number of ways to achieve the desired result. For this, we have already seen that a dynamic programming solution already exists (Subtask 1). Trying the above greedy approach can be very bad in this case, a simple example being $(S = 99999999999, N = 108)$.

With some of the above ideas, we design a simple branch and bound based algorithm for the problem:

    range_tried = [0 for i in [1, len(S) - 1]]
    # Find all range in S such that their value is less than N and sort
    # them in decreasing order of their value. Let it be called "RANGES"

    def recurse(range_idx, remain):
        if remain < 0:
            return false
        if remain < LIMIT:      # LIMIT ~ 100000
            use dp based subtask_1 solution
        else:
            for i in [range_idx, len(RANGES) - 1]:
                if conflict(current_range, range_tried):
                    # If current range we are trying conflicts with one
                    # already tried in recursion before.
                    continue

                X = value of integer for RANGES[i]
                # Update range_tried
                if recurse(range_idx, remain - X):
                    return True
                # Update range_tried to old value
        return False

Note the above is a simple solution based on the initial observations. But do we need to really check for all possible ranges? Can we decide greedily at some point that given range can never result in an answer as $N$, i.e. Say we have selected some ranges, can we say that with the remaining ones we can never achieve the target $N$ without checking all possible partitions or greedily checking large number ranges.

Actually, given initial choice of our ranges, we can bound the maximum number we can achieve with the remaining ones. A simple check which ignores the digits of remaining parts of $S$ and considers all of them to be $9$ and finds the maximum value possible is a good starting point. If this value is already less than $N$, then we can simple prune our solution. Even stronger checks based on actual values of digits in string $S$ can lead to better pruning. So, the loop in the above code modifies as follows:

    for i in [range_idx, len(RANGES) - 1]:
        if conflict(current_range, range_tried):
            # If current range we are trying conflicts with one
            # already tried in recursion before.
            continue
        MAX_POSSIBLE = get_max(ranges_set)
        if MAX_POSSIBLE < N:
            # As we iterate in decreasing order of numbers, the
            # MAX_POSSIBLE can only decrease as 'i' increases
            break

        X = value of integer for RANGES[i]
        # Update range_tried
        if recurse(range_idx, remain - X):
            return True
        # Update range_tried to old value

Another thing we can do is to remove the early exit of recursion where a check is based on "remain < 0". This can be easily done by directly starting from ranges such that value of considered numbers is always less than "remain". This is again helpful as after greedily choosing a large size partition, it is possible in most case the other large size partitions should be ignored in further recursion either due to conflicts in common ranges or "remain" decreasing too fast to become less than $0$. For this, a simple binary search can help us to find the first index in "RANGES" from where we should begin our search. This is possible as we had initially stored our ranges in decreasing order of the value of integers they represent.

With the above ideas, the recursive solution based on branch and bound works quite fast in practice. A small analysis of the time complexity is as follows:

1. $N < 100000$: Assuming we set LIMIT to this value in above pseudo-code. A dynamic programming based solution is run with complexity $O(|S| * N)$. Again to optimise this, we can use recursive version instead of iterative version. This is because will work in exactly the above complexity but in recursive solution, most of the states will be unvisited due to our initial choices of the ranges. This will significantly reduce the constant factor in your code.

2. For most of the other cases, as $N$ becomes larger i.e. size $n$ reaches closer to $|S|$, the possible solutions reduce significantly as explained before.

A more detailed analysis of time complexity is will available soon.

Ashmelev solution (Fastest in the contest): Branch and Bound with strong bound checking

Tips for Big integer library (mostly for C++ users)

Languages like python and java already have big integer library implemented in them. But C++ users need to implement the same for their usage in this problem. A small tip is to store the numbers as groups instead of single digits. For example: $S = 123456789123456789$. Below are 2 possible ways to store $S$:

$$S = 1|2|3|4|5|6|7|8|9|1|2|3|4|5|6|7|8|9$$

$$S = 123456|789123|456789$$

This helps to perform operations on base different than 10 and reduces the constant factor of your program. Generally, the base is chosen as ${10}^{9}$ so that all possible operations like $(+, -, * , /)$ fit inside the datatypes provided by the language. You can see setter's library for example.

Time Complexity

To be described in detail later.

Space Complexity

To be described in detail later.

Solution Links

The solution for subtask 1 can be found here

Setter's solution can be found here

Ashmelev's solution can be found here

[Open For Discussion] -

Today I was going through Somewhat suspicious coderkgcstar and kutengine competing in teams? . I'm not interested in raising issue again.

Since CodeChef's Code Of Conduct Says -
You may try to solve a problem as a team, but then make sure that there is only one submission made for a discussed solution in a contest. Submitting the same solution (even algorithm) by the different members of the team or a discussion group is not fair and will be considered as plagiarism.

Instead If we also have team registration option in long, cook and lunchtime. Due credit can be given to all members. If few individual's register/participate as a team. Then if a individual tries to submit from his personal account (accidentally), pop up can be shown to him that you are not allowed. This can save team from plagiarism hammer.
This will also help teams for preparations for ACM-ICPC. Ultimate objective of CodeChef

My point is If it is allowed then why there is no way to register/participate as team ??

And I cannot find any button for creating a team. Only method I found I look for upcoming team contest. And register for that contest after creating team. Does there exist any method to register team other than this.

P.S. - Contest like IOITC181 should have a team participation option.

Hi, http://codeforces.com/contest/992/submission/39398812http://codeforces.com/contest/992/submission/39398568

these were the codes submitted by me for the codeforces contest..but it is showing some strange error while it runs perfectly on ide.can you help me to figure this error..thanks in advance.

PROBLEM LINK:

Practice

Author:Arjun Bharat
Tester:Arjun Bharat
Editorialist:Arjun Bharat

DIFFICULTY:

EASY-MEDIUM

PREREQUISITES:

Math, modular exponentiation

PROBLEM:

Given the functional equation f(x+1)=kf(x)+g(x), g(x+1)=kg(x)+f(x), f(0)=2 and g(0)=0, the task is to find the value of f(n) modulo 1000000007, where n and k are program inputs.

QUICK EXPLANATION:

This is achieved by first solving the equations to obtain: f(x)= 2^x, if(k=1)f(x)= (k+1)^x + (k-1)^x, for k>1. Then we compute the remainder using fast modular exponentiation which is best suited for the given constraints.

EXPLANATION:

One may either add or subtract the two equations and obtain these following equations: f(x+1)-g(x-1)=(k-1)(f(x)-g(x)),f(x+1)+g(x+1)=(k+1)(f(x)+g(x)) Thus defining new functions h(x)=f(x)+g(x) and p(x)=f(x)-g(x), we have p(x)=2*(k-1)^x, h(x)=2*(k+1)^x. Substituting any one of them back will yield f(x+1)=(k+1)f(x)-(k-1)^x, and thus by superposition of the homogeneous and particular solutions to the recursive relation, set f(x)=a(k+1)^x + b(k-1)^x</sup***,> + (k-1)^x. Now we proceed to obtain the remainder.
Notice that using a linear recurrence, ans(n)=(k * ans(n-1))%M is O(n) and will not pass in under one second.
We proceed to use fast modular exponentiation. A brief snippet coded in C++ is highlighted below:
long long fn(long long n,long long k)
{
if(n==0)
return 1;
else if(n==1)
return k;
else if(n%2==0)
{
long long y = fn(n/2,k);
return ((y%M)(y%M))%M;
}
else
{
long long z= fn(n/2,k);
return ((y%M)(y%M)*(k))%M;
}
}
long long ans = fn(n,k+1)+fn(n,k-1);
ans%=M;//M=10^9+7
//This code works even when k=0, as the second call returns 0. This is O(lg n), a marked improvement.

ALTERNATIVE SOLUTION:

The trivial solution is to use a linear recurrence as described earlier, which is not suitable based on program constraints.
Manually computing and storing f(x) and g(x) values, with or without modulo is not advisable due to their large magnitudes, and the linear time complexity involved therein.

AUTHOR'S AND TESTER'S SOLUTIONS:

Author's solution can be found here: jdoodle.com/a/wPF

RELATED PROBLEMS:

TOPTWO

PROBLEM LINK:

Practice

Author:Arjun Bharat
Tester:Arjun Bharat
Editorialist:Arjun Bharat

DIFFICULTY:

EASY-MEDIUM

PREREQUISITES:

Hashing, implementation

PROBLEM:

Given a string of length n consisting of only lowercase characters, subject to m pairwise character interchange operations, obtain the final state of the message.

QUICK EXPLANATION:

It suffices to apply the interchange operation on the identity alphabet string, "abcdefghijklmnopqrstuvwxyz".
This is because each original character of the alphabet is always mapped to the index corresponding to it's ASCII value in the identity string(eg. c is mapped to ASCII(c)-97=index 2).
Thus replacement operations are O(m) and the final printing operation is O(n).

EXPLANATION:

A sample snippet of the code used is shown below: //Replacement operation coded in cpp14
for(i=1;i<=m;i++)
{
char p,q;
cin>>p>>q;
for(j=0;j<26;j++)
{
//a denotes the alphabet string, abcdefghijklmnopqrstuvwxyz
if(a[j]==p)
a[j]=q;
else if(a[j]==q)
a[j]=p;
}
for(i=0;i < n;i++)
printf("%c",a[message[i]-97]);
To print the string we print the character at the index of it's mapping in the alphabet string, since the index to which every character of the alphabet is mapped is an invariant.

ALTERNATIVE SOLUTION:

Brute force would apply each interchange operation on the original string,which is O(nm) in overall complexity. This is not feasible given the program constraints.

AUTHOR'S AND TESTER'S SOLUTIONS:

Author's solution can be found here: jdoodle.com/a/wQx

A recurrence relation of this type: $F_n = 2F_{n - 1} + 3F_{n - 2} + 3$ , where sum of the coefficient of recurring terms on both side of the equation is not equal.

I have seen a codechef video ( by Kevin ) where they explain the offset adding to solve this type of recurrence by removal of the constant term. The recurrence can be converted to $G_n = 2G_{n-1} + 3G_{n-2}$ and later use matrix exponentiation to solve it with matrix $\begin{bmatrix} 2&3\\ 1&0\\ \end{bmatrix}$ to obtain the value of $G_n \textit{ mod }M$. For example,

$\begin{align*} &\text{Let, }F_n = G_n + C\\ &\Rightarrow G_n + C = 2\left [ G_{n - 1} + C \right ] + 3\left [ G_{n - 2} + C \right ] + 3 \\ &\Rightarrow G_n + C = 2G_{n - 1} + 3G_{n - 2} + 5C + 3 \\ &\Rightarrow G_n= 2G_{n - 1} + 3G_{n - 2} + 4C + 3 \\ &\Rightarrow C = -\frac{3}{4} \\ \end{align*}$

Now after calculating the value of $G_n \textit{ mod }M$ how to recover $F_n$?

Thanks!

https://www.codechef.com/viewsolution/18944558

Can someone please help me in finding the error? I am getting correct ans for test cases but getting wrong ans on submitting.

PROBLEM LINK:

Practice

Author:sriram10
Tester:sriram10
Editorialist:sriram10

DIFFICULTY:

MEDIUM

PREREQUISITES:

Graphs, depth first search (DFS), topological sort, dynamic programming (DP)

EXPLANATION:

Firstly, if there is a cycle, then the answer would be arbitrarily large, as you could keep returning to a particular vertex and collect stones of the same colour. To find if a cycle exists, you can run a DFS on the graph.

Otherwise, the graph becomes a Directed Acyclic Graph. Now, we compute the maximum score by using DP. We first topologically sort the vertices. The DP is computed this way: Let $DP[i][j]$ indicate the maximum score when the player starts from $i^{th}$ vertex and collects the stones of colour code $j$. Now, if $i$ has no outgoing vertex, i.e. it is the leaf of topological sort, then $DP[i][a[i]]=1$ and $DP[i][j]=0$ for $j!=a[i]$. For all other nodes, $DP[i][j]=max(DP[v][j])$ for all $v$ adjacent to $i$, for every colour $j$. Also, we need to increment $DP[i][a[i]]$ by 1 after the previous process is done. Later, we could print the highest value in the DP table.

AUTHOR'S SOLUTION:

Author's solution can be found here.

PROBLEM LINK:

Practice

Author:shay_gan
Tester:shay_gan
Editorialist:shay_gan

DIFFICULTY:

EASY-MEDIUM

PREREQUISITES:

Modular arithmetic

EXPLANATION:

The question is actually deceptively easy. If we have $M$ lanes and $M^K$ horses, finding the top two requires the following steps.

1. Finding the fastest horse.
2. Finding the $2^{nd}$ fastest.

Since unless we know the fastest, we cannot find the $2^{nd}$ fastest, it is seen that the $2^{nd}$ step must necessarily complete after the first. Among $M^K$ horses, finding the fastest is easy - race them $M$ at a time, and the winners move on. Since $M^K$ horses are there and each race eliminates $M-1$ horses (since only one horse moves on), the required number of races for this part is $(M^K-1)/(M-1)$. No race will have less than $M$ horses, so the solution must be optimal. Now for the $2^{nd}$ fastest, we need to compare every horse that came $2^{nd}$ in a race the fastest won. Clearly there will be $K$ such horses. To find the fastest of these we just need $ceiling((K-1)/(M-1))$ races.

So the answer is $(M^K-1)/(M-1) + ceiling((K-1)/(M-1))$.

Note: In general, to implement the ceiling function easily while coding, you can use the fact that $ceiling(x/y) = floor((x-1)/y)+1$.

Code in Python: Due to no limit on integer length, we can directly find the answer and apply modulo $10^9+7$

Code in C++: Must do it stepwise due to storage constraints, but it is faster.

Also, as illustrated in this C++ code, without running the loop to calculate $1+M+M^2+...+M^(k-1)$, you can directly calculate $(M^K-1)/(M-1)$ by calculating the modular inverse of $M-1$ under modulo $10^9+7$ using Fermat’s Little Theorem. Both solutions would pass though.

PROBLEM LINK:

Practice

Author:ranjithganesh
Tester:ranjithganesh
Editorialist:ranjithganesh

DIFFICULTY:

EASY-MEDIUM

PREREQUISITES:

Trees, Depth-First Search (DFS)

EXPLANATION:

The family can be viewed as a tree as given in the question and an individual's net worth as the value of the corresponding node. One simple observation that can be made is that if the maximum difference in net worth in the tree is between nodes $u$ and $v$, where $v$ is a descendant of $u$, then $v$ must either be the node with maximum value or minimum value in the subtree of $u$. Since the difference in values is to be considered only among its descendants, DFS can be performed which visits the root of all subtrees using recursion and returns the min-value and max-value of its subtree.

The returned min and max values of its descendants can be used to find the max difference in value with the root of the subtree. The final answer will be the maximum of the calculated value among all the nodes.

AUTHOR'S SOLUTION:

Author's solution can be found here.

PROBLEM LINK:

Practice

Author:sathu19
Tester:sathu19
Editorialist:sathu19

DIFFICULTY:

EASY-MEDIUM

PREREQUISITES:

Dynamic Programming, Binary Search

EXPLANATION:

Consider the arrangement 10, 163, 89, 5, 73, 15, 49. To get the final arrangement in ascending form, we need to move blocks 73, 89, 10 and 163. If you observe carefully the remaining blocks 5, 15 and 49 form an increasing subsequence. In fact, this is the longest increasing subsequence. The minimum number of blocks to be moved to form an ascending arrangement will always be $N$ - (the length of the longest increasing subsequence).

For the descending arrangement, we should find the length of the longest decreasing subsequence. Considering the previous example, the unmoved blocks in the descending arrangement are 163, 89, 73, 15 or 163, 89, 73 , 49. The length of the longest decreasing subsequence is 4, i.e the minimum number of blocks to be moved in this case is 3. Hence, Sriram’s arrangement will be used in this case.

To find the longest increasing/decreasing subsequence it takes time complexity $O(N^2)$ through the dynamic programming solution. Since $N$ can go upto $10^5$, a solution with this approach would not pass within the given time limit of 1 second. However, we only require the length of the longest increasing/decreasing subsequence. Finding the length of the longest increasing/decreasing subsequence takes time complexity $O(Nlog(N))$. Please refer to this link for the algorithm to find the length of the longest increasing subsequence. To find the length of the longest decreasing subsequence, we just reverse the array and apply the above algorithm again.

AUTHOR'S SOLUTION:

Author's solution can be found here.

So due to some small mistake a while ago when my rating was dropped by around 500 points for plagiarism in a really old contest, I didnt say anything. I gave the June Long Challenge and to my surprise, despite having 500 points and a ranking of 71, I got an increase of just 200 points, while some other people of my college, some having solved only 2 questions got a boost of 175 points. Is there any basis behind this? What's the point of a lower rated person even solving the questions in long challenges then? Someone please look into this as I am not the only one pissed off by this.