Hello,

Firstly, heartiest congratulations and best wishes to all the teams who qualified for the snackdown elimination round(Or are going to qualify :P ). This is the first time I have qualified and I am a bit excited.
I have a personal question for the teams. If the members of the teams are not physically with each other then how would they establish an effective mode of communication?

Now, a more general question: The problems in these ICPC-like(Snackdown elimination or cook-offs) contests are not sorted in any order of difficulty like normal codeforces rounds. What is the best strategy that the top performers use to know which is the easiest problem? Is it luck? Is it intuition? I don't think its effective to read all the statements before starting, or else there is no way a team solves the first problem in less than 5 mins.

Thank you. :)

new to data structures and algos, please provide me with links with videos and a place where everything is combiningly given

I have got a certificate for my participation in SNACKDOWN 2017. I want to add it to my linkedin profile. I am facing few problems. Please instruct me to do so. Thank you.

PROBLEM LINK:

Practice
Contest

Author:Dmytro Berezin
Primary Tester:Misha Chorniy
Editorialist:Hussain Kara Fallah

DIFFICULTY:

Cakewalk

PREREQUISITES:

None

PROBLEM:

Given a sequence of N arithmetic signs ( = , + , - ) between N+1 unknown integers. You are allowed to fix these integers using numbers in the range [1,P] such that the expression is true when you read it from left to right. (Numbers don't violate the signs). You are asked to calculate minimum possible P such you can construct a valid expression.

EXPLANATION:

First of all, it's clear that we can drop all '=' signs and pretend that they never existed, because each number which follows an '=' sign would be identical to the number preceding this sign. So these signs aren't affecting our answer at all. After discarding all '=' signs our answer would be :

P = max(maximum number of consecutive '<' signs, maximum number of consecutive '>' signs) + 1

Let's process our expression from left to right, If we are facing X (X ≤ P-1) consecutive '<' signs, our starting number would be P-X, and we increment our last number by 1 after each sign,so the number after the last sign would be exactly P (which will be followed by '>' sign). Our last number will be followed by Y consecutive '>' signs, so we assign the next number to Y (Y < P) and we decrement the last number by 1 by each '>' sign we process. The number after the last sign would be 1. (In case our expression starts with '>' the situation would just be reversed). After that we would have another block of Z consecutive '<' signs, so we assign the next number to P-Z (P-Z ≥ 1) so the number after the last sign would be P and we continue....

Following this approach, the last number after a block of consecutive '<' signs would be P (the maximal value), and the last number after a block of consecutive '>' signs would be 1 (the minimal value). So according to our bold assumption below we can assign values using numbers in the range [1,P] without violating the signs.

Let's take an example:

<<<=>=>=>>><<>>>><<<<<>><<>>

After removing = signs our sequence would be

<<< >>>>> << >>>> << >>>>>

(Blocks are separated by spaces for clarity)

here P = max(3 , 5 , 2 , 4 , 5 , 2 , 2 , 2) + 1 = 6

Our sequence would be

3< 4 < 5 < 6> 5 > 4 > 3 > 2 > 1< 5< 6> 4> 3 > 2 > 1< 5< 6 > 5 > 4 > 3 > 2 > 1

AUTHOR'S AND TESTER'S SOLUTIONS:

TESTER's solution: Will be found here
EDITORIALIST's solution: Will be found here

Guys, Can anyone suggest how to get 100 pts on this one ??(I have used a hash map)

https://www.codechef.com/viewsolution/14622106

PROBLEM LINK:

Practice
Contest

Author:Vineet Paliwal
Tester:Roman Rubanenko
Editorialist:Jingbo Shang

DIFFICULTY:

EASY

PREREQUISITES:

Sort, Priority Queue, Binary Search

PROBLEM:

Given two arrays A[1..K], B[1..K], deal with Q queries of finding the n-th smallest pair sum in all K^2 pair sums (A[i] + B[j]).

EXPLANATION:

A brute force enumeration can give us an O(K^2 logK) - O(1) algorithm: just simply store all possible sums and use the some sorting algorithm such as quick sort. And then, for each query, return the n-th number of the stored sorted array. This brute force algortihm’s time complexity is O(K^2 + Q). Also, it needs O(K^2) space. Both time and memory are exceeded.

There are 2 ways to improve this brute force algorithm. The common key point to improve this brute force algorithm is as following: Suppose A[] and B[] are sorted ascendingly, A[i] + B[j] is smaller than or equal to any A[i] + B[k] if k > j.

For instance, we use quick sort to sort A[] and B[] in O(K logK) time. And then, 2 possible solutions are here.

The first solution is that we can find the smallest sum among at most K candidates (one for each A[i]) and remove it. After n removes, the n-th smallest sum is found. More specifically, we can maintain K pointers for each A[i]. Let’s say ptr[1..K] (equals 1 initially). First, we can use a binary heap (or other priority queues, balanced binary search trees, etc...) to find the smallest sum among A[i] + B[ptr[i]]. Second, suppose the smallest is A[p] + B[ptr[p]]. We remove it from the heap, then increase the pointer ptr[p] by 1 and insert a new element A[p] + B[ptr[p]] if it exists. Repeat this process n times, the n-th smallest sum is got. This algorithm’s time complexity is O(n log K) for each query, and thus O(K logK + Q n logK) in total.

The second solution is more tricky and useful. Consider the dual problem: given a number X, find how many pair sums are smaller than or equal to X (The answer of the original problem is that the smallest X such that there are at least n pair sums smaller than or equal to X). To solve the dual problem, based on the previous observation, there exists limit[i] such that A[i] + B[1..limit[i]] are all smaller than or equal to X while A[i] + B[limit[i] + 1 … K] are all greater than X. Furthermore, limit[i] >= limit[i + 1] since A[i] <= A[i + 1]. Using these two properties, we can simply get the rank of X in O(K) time. Through binary search, we can get the answer of original problem in O(K logAnswer), and thus O(K logK + Q K logAnswer) in total.

AUTHOR'S AND TESTER'S SOLUTIONS:

Author's solution can be found here.
Tester's solution can be found here.

<code>
#include <iostream>
using namespace std;

int main()
{
    int t;
    cin>>t;
    while(t--)
    {
    float c;
    long int h,ts;
    cin>>h>>c>>ts;
    if(h>50&&c<0.7&&ts>5600)
    {cout<<"10"<<endl;}
    else if(h>50&&c<0.7)
    {cout<<"9"<<endl;}
    else if(c<0.7&&ts>5600)
    {cout<<"8"<<endl;}
    else if (h>50&&ts>5600)
    {cout<<"7"<<endl;}
    else if ((h>50 &&c>=0.7 && t<=5600)||(h<=50 && c<0.7 && t<=5600) ||(h<=50 && c>=0.7 && t>5600))
    {cout<<"6"<<endl;}
    else
    {cout<<"5"<<endl;}
    }
    return 0;
}

Can anyone please help me in understanding how to take input in problems like these which do not specify the number of test cases?

https://www.codechef.com/viewsolution/14624679

PROBLEM LINK:

Practice
Contest

Author:Aleksandr Kulkov
Primary Tester:Misha Chorniy
Editorialist:Hussain Kara Fallah

DIFFICULTY:

Medium

PREREQUISITES:

Combinatorics,Math,Number Theory

PROBLEM:

Consider an ordered tree with N vertices. Your task is to calculate the expected value of the number of vertices having exactly one child in such tree assuming that it is uniformly chosen from the set of all ordered trees of size N.

Consider the answer to be a proper fraction P/Q, where gcd(P, Q) = 1. Then your task is to output two integers PQ^-1 mod 10⁹+7 and PQ^-1 mod 10⁹+9

EXPLANATION:

OBSERVATION 1:

The number of ordered trees consisting of n nodes is equal to the (n-1)^thcatalan number. Imagine the Depth-First-Search order of the nodes of the trees, entering each node corresponds to an open bracket ( , and finishing each node corresponds to a closed bracket ) . So if we represented the DFS order of a tree it will form a simple balanced bracket sequence.

Two different ordered trees must have different bracket representations. So we can say that the number of ordered trees consisting of n nodes is equal to the number of balanced bracket sequences consisting of (n-1) pairs of brackets. (n-1) because our tree is connected so we must fix the root (the first and the last bracket in the expression). If the subexpression (the expression excluding the first and last bracket) is balanced, that guarantees that we will never exit the root before the last bracket and our tree is connected.

It's well known that the number of balanced bracket sequences of n pairs of brackets is equal to the n^th catalan number.

$C_n = \frac{(2n)!}{(n+1)!n!}$

Before reading the next observation you should be familiar with Linearity Of Expectation.

OBSERVATION 2:

Let's consider all different (n-1) ordered trees, and think about applying this operation. Choosing an arbitrary node of a tree and linking it to a single child(n^th node) and removing all edges between our chosen node and its children, then linking them to our new node. So our new node would serve as a single child of the chosen one.

A node having one child in a tree is equivalent to a pair of brackets, with a balanced expression between them and surrounded by a pair of brackets.

Observe that each node in a tree consisting of n nodes and having only one child can be formed by applying this operation to only one tree of (n-1) nodes. It's exactly the same as choosing an opened bracket and its corresponding closing bracket in a simple balanced bracket sequence framing the subexpression between by a pair of brackets (our new node).

Thus our nominator P would be

P = ( number of trees of n-1 nodes * (n-1) )

We multiplied by n-1 which denotes the number of ways to choose the vertex we decided to apply this operation on.

Q = ( number of trees of n nodes )

$answer = \frac{C_{n-2} * (n-1)}{C_{n-1}}$

According to the catalan number formula we wrote above, this can be reduced to:

$answer = \frac{n * (n-1)}{4n-6}$

This fraction can be reduced easily by calculating GCDs between the denominator and the nominator terms. We can calculate PQ^-1 after calculating the modular inverse of Q considering each modulo.

Note:

It's true that this solution is given without a formal proof. But the idea is quite simple and correct. Actually its correctness can be proved by intuition. In real life contests you won't have the internet to read formal proofs and papers or search for formulas for a sequence. This solution is not hard to get from scratch and worths trying.

AUTHOR'S AND TESTER'S SOLUTIONS:

AUTHOR's solution: Will be found here
TESTER's solution: Will be found here
EDITORIALIST's solution: Will be found here

My Rating Decreased by 183, even tough I am getting "You did not participate in this contest" and there is no section for Cook83 under Problems Solved on my Profile.

 public class GuessGame {
 Player p1;
 Player p2;
 Player p3;

The following code, when put into eclipse says that '

person can't be resolved to a type

' although it is given in the book head first java as a code example.

hola comunidad, espero que si alguien tiene la solucion a mi problema me ayude :), para los problemas planteados en la pagina de practica utilizo mi editor de codigo el idle de python por defecto, mi version de python es 3.6, en mi idle todo anda correctamente con el codigo, pero cuando lo subo a la pagina para chequear si la respuesta es valida o no esta me tira un error, los codigos que he acertado tambien usan esta version de python, pero quisiera saber si es por la diferencia de versiones de python (entre la que uso yo y la que usa la pagina), estoy atento a cualquier ayuda si me dan criticas "constructivas" en cuanto a mi codigo mejor, gracias de antemano :-)

Can anyone find the error in following code

import java.util.; import java.io.; class petrol{ public static void main(String arg[]) { Scanner sc = new Scanner(System.in); int n; int[] i = new int[100]; int x,y,j=1; float t,s; n=sc.nextInt(); n = n*3; while(j<=n) { i[j] = sc.nextInt(); j++; } j=1; while(j<=n) { x=i[j]; y=i[j+1]; s=i[j+2]; if(x==0 && y==0) { System.out.println(0); } else { t=s/(x+y); System.out.println(t); }

        j=j+3;
    }
    }

}

pycharm is giving me an error : not enough values to unpack(expected 2 but got 1) while codechef is accepting it.

why is pycharm or any other ide giving an error?

Hey Guys,I am getting TLE on a very basic and simple problem(feel bad for that)...I've tried the same logic of the code cramped into the main method hopin it would run faster but it took even more. The Problem TWONUMS. https://www.codechef.com/problems/TWONMS The original constraints are 1 sec and 50k bytes and the testcases are upto 100.

And somehow my code executes at 0.11 millisec at its best, and considering the codechef stress test(that is it will run the maximum number of testcases)..if i could reduce the execution time to 0.1 it would work. And i couldnt figure what i can possibly reduce with the code. Please do comment on my Coding prefrences or in anyway i could improve. Any critics are highly encouraged.

import java.util.Scanner;

void getData()
{
    int num_alice = sc_ops.nextInt();
    int num_bob = sc_ops.nextInt();
    int turns = sc_ops.nextInt();
    gameplay(num_alice,num_bob,turns);
}


void gameplay(int num_alice,int num_bob,int turns)
{
    for(int i=1;i<=turns;i++)
    {
        if(i%2==0)
        num_bob*=2;
        else
        num_alice*=2;
    }
    result(num_alice,num_bob);
}

void result(int num_alice,int num_bob)
{
    //result=Math.max(num_alice,num_bob)/Math.min(num_alice,num_bob);
    result=(num_alice>num_bob)? (num_alice/num_bob):(num_bob/num_alice);
    System.out.println(result);
}

    while(cases--!=0)
    {
        obj.getData();

    }


}

}

PROBLEM LINK:

Practice
Contest

Author:Anudeep Nekkanti
Tester:Minako Kojima
Editorialist:Lalit Kundu

DIFFICULTY:

EASY

PRE-REQUISITES:

Sorting, Greedy

PROBLEM:

You have to buy N items of cost A₁, A₂ ... A_N. For every two items you buy, they give you two items for free. However, items can be of varying price, they always charge for 2 most costly items and give other 2 as free. For example, if the items cost 1, 1, 2, 2, then you have to pay 4 and take all 4 items.
Find minimum price in which you can buy all items?

QUICK EXPLANATION:

Sort the array A and greedily start choosing from largest elements.

EXPLANATION:

Claim 1:

We should pick the most costliest and second most costliest items in a single bill.

Proof:

Assume x be the most costliest item and y be the second most costliest item. Assume x and y are in different bags. There can be two cases.
- The bag containing x, has only one element.
We can add y in the same bill too because we are anyway paying for both, so why two separated bills instead of one.
- The bag containing x, has more than element. Assume z be the second most costliest item in bag containing x.
Now we can simply swap y and z. So we will end up x and y being in same bag. Also due to this swapping, there is no change in cost because we were anyway paying for both x and y before.

After picking the most costliest items in a single bill, we should try to pick the third and fourth most costliest items also in the same bag to get most benefit of buy 2, get 2 free scheme. As the third and fourth items will be free.
We can even formally prove this part similar to swapping item used in previous claim.

This concludes the mathematical proof required.

Now that we have chosen one group we'll choose further groups from remaining array A.

This is the design of our greedy algorithm. We sort the array A first and then start choosing groups of 4 in decreasing order of array A. This will ensure that we make minimum sum.

Pseudo code:

A = input
sort(A)
reverse(A)
ans = 0

for i=0 to N-1:
    //count in answer the index 0,1,4,5,8,9...
    if i%4 < 2:
        ans += A[i]

print ans

Complexity: O(N log N) due to sorting.

SOLUTIONS:

Setter's solution
Tester's solution

Hello Coders,

Hope you are having a great time coding hard. Here I present to you a Utility tool - StopStalk which will encourage you to keep your algorithmic progress going by coding with your friends and improve.

It retrieves your friends’ recent submissions from various competitive websites (CodeChef, Codeforces, Spoj, HackerEarth, HackerRank and UVa Online Judge for now) and shows you in one place. It includes lots of other features like - User streak notification, Global Leaderboard, Filter submissions, search problems by tags, Trending problems across these sites, Unified Todo list, View/Download submissions directly and a lot more…

You can add friends who are already on StopStalk or you can also add a Custom User and start coding collectively by keeping a close watch on your algorithmic progress as compared to that of your friends.

If you want to increase your Custom User limit, you can share your StopStalk handle and you can get 1 extra user for every 3 users who register with your handle as Referrer's StopStalk handle.

Register here - StopStalk

The goal is to involve more and more people to Algorithmic Programming and maintain their streak. Also the project is completely Open Source - Github

Feel free to contribute. :)

We would be happy to hear from you - bugs, enhancements, feature-requests, appreciation, etc. In the end - Stop stalking and start StopStalking! Happy coding!

EDIT: 3500+ users already registered globally :) (Thanks a lot guys for your love!)

I have been trying to solve the Gross Salary(FLOW011) problem under beginner section. I have written a code which is working fine for the inputs given in the page but the codechef compiler is showing error, can someone please point out the error.

(UPDATED) Still it's giving same error. Here is the code.

   import java.util.Scanner;

class Flow011 {
public static void main(String[] args){
    Scanner in = new Scanner(System.in);
    double n = in.nextDouble();
    while(n-->0){
        int  salary = in.nextInt();
        double gross;
        if(salary<1500){
            gross = salary+(salary*0.1)+(salary*0.9);
        }
        else{
            gross = salary + 500 + (salary*0.98);
        }
        if(gross==Math.floor(gross)){
            System.out.println((int)gross);
        }
        else
        System.out.printf("%g\n",gross);
    }

    in.close();
}
}

PROBLEM LINK:

Contest
Practice

Author:Istvan Nagy
Tester:Kevin Atienza and Gedi Zheng
Editorialist:Kevin Atienza

PREREQUISITES:

Tree center, tree radius, tree diameter, breadth-first search

PROBLEM:

The diameter of an undirected graph is the largest distance between any two nodes in the graph.

Given an unrooted tree, is it possible to decrease the diameter by adding exactly one edge?

QUICK EXPLANATION:

Handle the special case $N = 2$ (the answer is "NO"). In the following, assume $N > 2$.

First, find the centers of the tree (in $O(N)$ time). There can be one or two centers.

• If there is only one center, root the tree at the center, and compute the height of each subtree. Let $H$ be the height of the tree. Print "YES" if the root has exactly two children with height $H-1$, otherwise print "NO".
• If there are two centers, remove the edge connecting the centers to form two trees, root the two trees on the centers, and compute the heights of all subtrees. Let $H$ be the (common) height of both trees. Print "YES" if one of the roots has exactly one children with height $H-1$, otherwise print "NO".

EXPLANATION:

Let us first define a few simple terms related to trees and graphs.

The eccentricity of a node is the largest distance from that node to any other node in the graph.

The diameter of an undirected graph has been defined already. It is the largest distance between any two nodes in the graph. Alternatively, it is the largest eccentricity of any node in the graph. We also call any longest path in the graph a diameter, so the term "diameter" can mean either a path or a number, and it will be clear in context which kind of "diameter" we are referring to.

The radius of an undirected graph is the smallest eccentricity of any node in the graph.

A center of an undirected graph is any node whose eccentricity is equal to the radius. Note that a graph can have many centers (in particular, in a complete graph, all nodes are centers).

Since unrooted trees are a special case of undirected graphs, all the above terms are also defined for them. However, in the case of trees, there are a few additional useful properties:

• If $R$ is the radius and $D$ is the diameter, then $R = \lceil D/2 \rceil$ (i.e. the radius is approximately half the diameter).
• A tree has either one or two centers.
• If there are two centers, then they are connected by an edge.
• All diameters pass through the center(s).
• The diameter is even if and only if there is one center.

These are pretty standard facts and are easy to prove, so we leave this exercise to the reader. The following illustrates the two cases, depending on the number of centers. The blue-filled nodes are the centers, and the blue edges are part of some diameter.

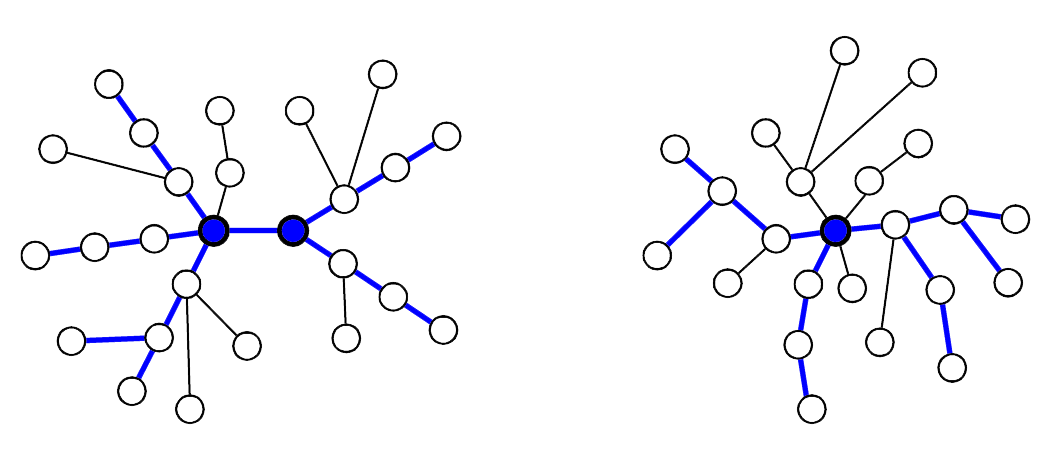
All in all, the facts above say that the circumstances are really nice for an unrooted tree.

Computing the answer

Let's see how the center, radius and diameter can help us in answering the question. Note that all diameters pass through the center(s), which means that we only have to care about decreasing the lengths of those paths. We handle two cases, depending on whether there are one or two centers.

Case 1: 1 center

Suppose that the tree only contains one center, say $C$. It makes sense to root the tree on $C$. Since the graph has at least two nodes, $C$ has at least two children (it cannot have just one, otherwise it wouldn't be a center). Furthermore, the height of the rooted tree is equal to the radius $R$ of the whole tree, and there are at least two direct subtrees of $C$ whose height is exactly $R-1$. These facts are intuitive and can easily be proven. See the following for a better picture of the situation:

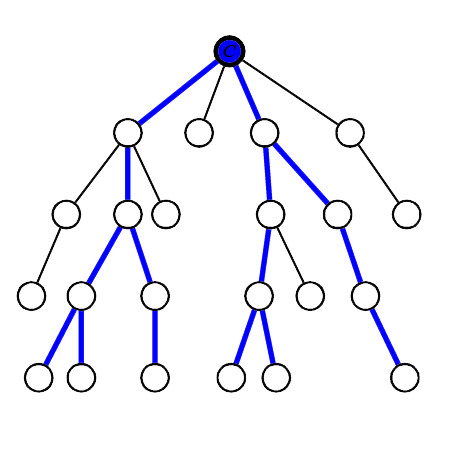
Suppose there are exactly two direct subtrees of $C$ with height $R-1$, say $A_1$ and $A_2$. In this case, all diameters pass through the sequence of nodes $A_1$-$C$-$A_2$ (or the reverse), and we can decrease the lengths of all these paths by adding an edge from $A_1$ to $A_2$, as shown below.

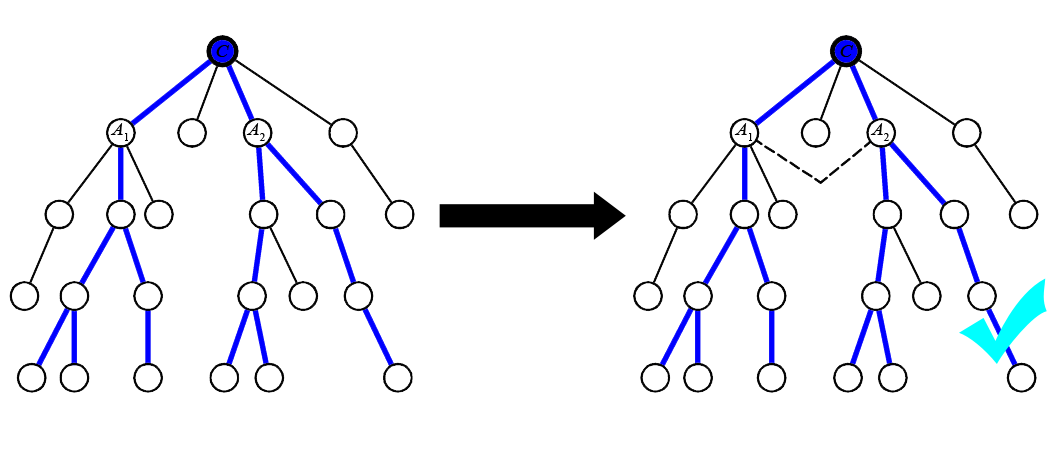
The paths passing through $A_1$-$C$-$A_2$ can instead take a shortcut by passing directly through the new edge, bypassing $C$. So we conclude that the answer is "YES" if $C$ has exactly two children with height $R-1$.

What if there are more than two direct subtrees whose height is $R-1$? Then in this case, we can show that it is impossible to add one edge to decrease the lengths of all diameters. This is because each diameter passes through exactly two of these subtrees, but by adding an edge, we only influence paths that pass through two subtrees, so diameters passing through the remaining trees are not affected.

This is illustrated in the following image, where there are three such children, $A_1$, $A_2$, $A_3$. In all the following cases, try to figure out why there are diameters which are not affected by adding the dashed edge.

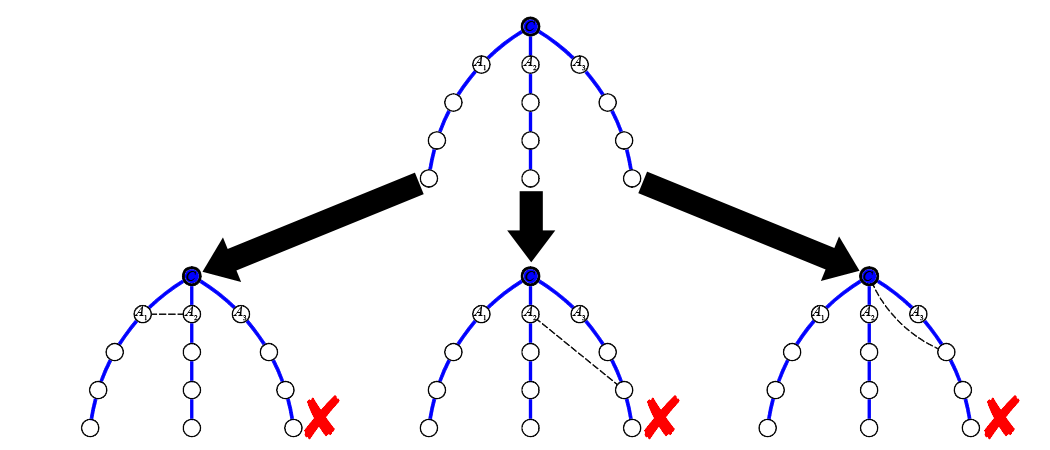
In fact, it is straightforward to prove this fact rigorously. Therefore, we conclude that the answer is "NO" if $C$ has more than two children with height $R-1$ :)

Case 2: 2 centers

We now turn to the case where there are two centers, say $C_1$ and $C_2$. In this case, there is an edge between $C_1$ and $C_2$. Let's ignore that edge first, and root the two resulting trees on $C_1$ and $C_2$.

Now, we're sure that $C_1$ and $C_2$ has at least one child each, unless the $N$ is exactly two. But if there are just two nodes, we can simply output "NO" (there is only one such case. In fact, this case is given as a sample input). Therefore, we can assume that $C_1$ and $C_2$ has at least one child each. We can also show that the heights of both trees are equal. Let $H$ be this common height (note that it is possible to show that $H = R-1$).

Proceeding as in the above, suppose that $C_1$ has exactly one child of height $H-1$, say $A$. Then in this case it is possible again to decrease the lengths of the diameters by adding an edge from $A$ to $C_2$, as shown in the following:

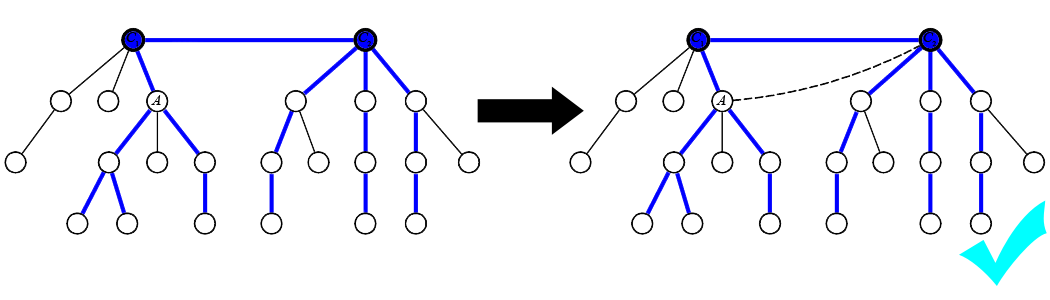
All diameters pass through the node-sequence $A$-$C_1$-$C_2$, but by adding the new edge, the diameters can bypass the node $C_1$. Therefore, if $C_1$ has exactly one child of height $H-1$, then the answer is "YES". A symmetric argument applies if $C_2$ has exactly one child of height $H-1$.

Now, what if $C_1$ and $C_2$ both have more than one children of height $H-1$? Then, similarly as in the previous case, we can show that it is impossible. Consider for example the following case:

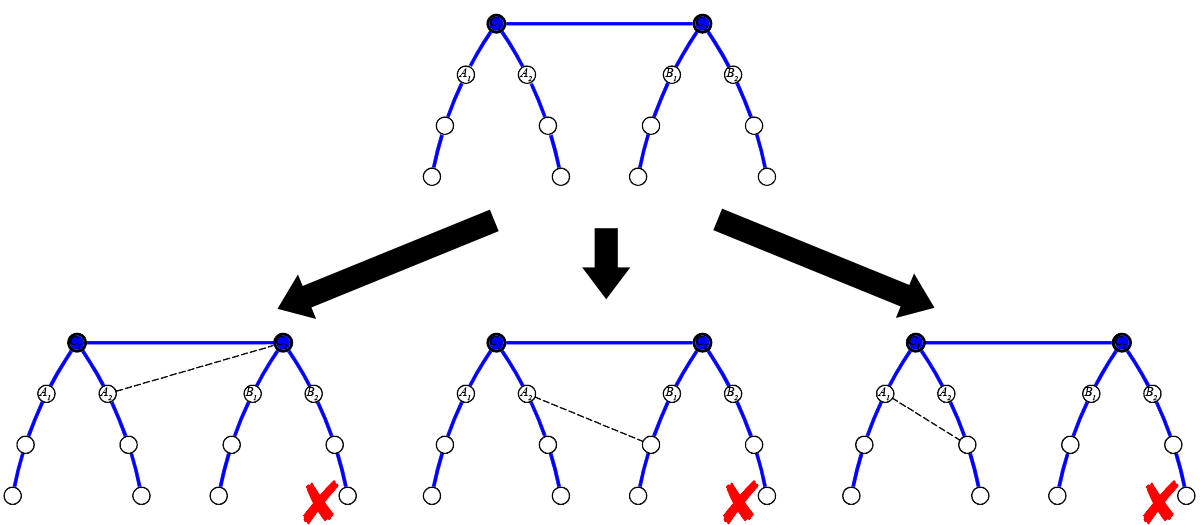
No matter where we place the edge, there are still diameters that are not affected by the new edge. Therefore, the answer is "NO".

We have handled all the possible cases, and our solution runs in $O(N)$ time (assuming we already know the centers of the tree). This is an optimal solution!

Computing the center

The above algorithm assumes that we have already computed the centers of the tree. How do we compute the centers? There are several well-known ways to do it, some of them running in optimal $O(N)$ time. We will discuss one here:

• Select an arbitrary node $X$.
• Find the farthest node $Y$ from $X$. If there is more than one, pick any.
• Find the farthest node $Z$ from $Y$. If there is more than one, pick any.
• The path $Y$-$Z$ is now a diameter, so the centers are the centermost nodes on the path from $Y$ to $Z$ (there can be one or two such nodes).

Clearly, this runs in $O(N)$ time. But why does it work? This algorithm relies on the following fact:

For any node, any farthest node from it is an endpoint of some diameter.

Proof:

Let $D(i,j)$ be the distance between nodes $i$ and $j$.

Let $X$ be any node, and $Y$ be any node with the maximum distance from $X$. We want to show that $Y$ is the endpoint of some diameter. There are two cases:

• The path $X$-$Y$ doesn't intersect any diameter.
• The path $X$-$Y$ intersects some diameter.

Let's handle them separately:

Case 1: The path $X$-$Y$ doesn't intersect any diameter.

In this case, let $A$-$B$ be any diameter. Let $W$ be the nearest node from $X$ that belongs in the path $A$-$B$, and let $V$ be the farthest node from $X$ in the path $X$-$W$ that still belongs in the path $X$-$Y$. Note that it's possible that the vertices described here are not distinct. However, we know that nodes $V$ and $W$ are distinct, by assumption. Therefore $D(V,W) = D(W,V) \ge 1$. The following image illustrates the situation:

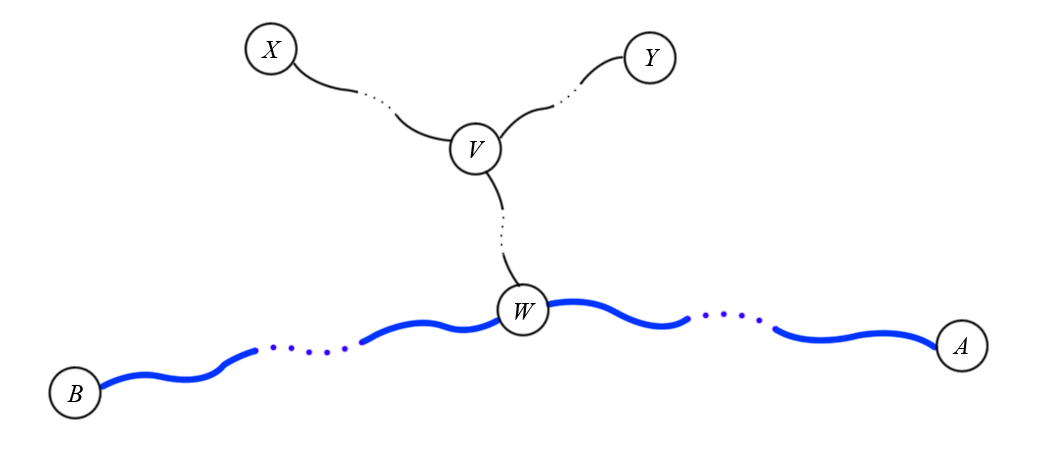
We will show that the path $B$-$Y$ is longer than the diameter, which is a contradiction (because the diameter is the longest path).

Since $Y$ is farthest from $X$, we have $D(X,A) \le D(X,Y)$. But we have $D(X,A) = D(X,V) + D(V,W) + D(W,A)$ and $D(X,Y) = D(X,V) + D(V,Y)$, therefore we have: $$D(V,Y) \ge D(V,W) + D(W,A)$$ and $$D(W,Y) = D(W,V) + D(V,Y) \ge D(W,V) + D(V,W) + D(W,A) \ge 1 + 1 + D(W,A) > D(W,A)$$ and finally $$D(B,Y) = D(B,W) + D(W,Y) > D(B,W) + D(W,A) = D(B,A)$$ which shows that $B$-$Y$ is indeed longer than the diameter $A$-$B$. This is a contradiction, therefore this case is impossible.

Case 2: The path $X$-$Y$ intersects some diameter.

This time, let $A$-$B$ be a diameter that intersects the path $X$-$Y$, and let $V$ and $W$ be the nearest and farthest nodes from $X$ in the path $X$-$Y$ that are in the diameter $A$-$B$, respectively. We also assume that $D(W,A) \le D(V,A)$, i.e. $W$ is nearer to $A$ than $V$ is unless $W = V$. There is no loss of generality, because otherwise we can just swap $A$ and $B$. As in the previous case, these nodes are not necessarily distinct. The following image illustrates the situation:

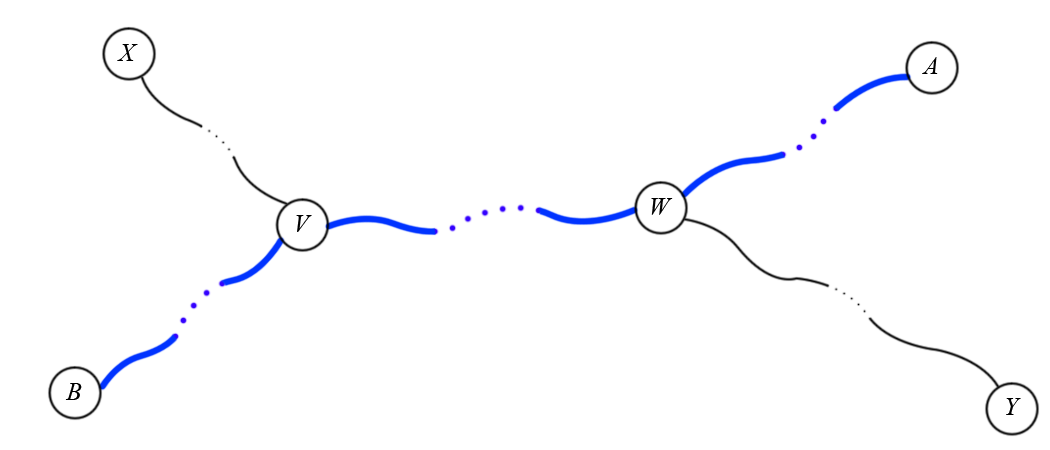
We will now show that the path $B$-$Y$ is also a diameter, which shows that $Y$ is an endpoint of some diameter.

Since $Y$ is farthest from $X$, we have $D(X,A) \le D(X,Y)$. But we have $D(X,A) = D(X,V) + D(V,W) + D(W,A)$ and $D(X,Y) = D(X,V) + D(V,W) + D(W,Y)$, therefore we have: $$D(W,Y) \ge D(W,A)$$ However, $$D(B,Y) = D(B,W) + D(W,Y) \ge D(B,W) + D(W,A) = D(B,A)$$ On the other hand, $D(B,Y) \le D(B,A)$ because $B$-$A$ is a diameter. Therefore, $D(B,Y) = D(B,A)$, and $B$-$Y$ is also a diameter, and we have shown that $Y$ is an endpoint of some diameter.

Time Complexity:

$O(N)$

AUTHOR'S AND TESTER'S SOLUTIONS:

Setter
Tester 1
Tester 2